题目内容
已知α、β∈(0,(1)将tanβ表示成tanα的函数关系式;
(2)求tanβ的最大值,并求当tanβ取得最大值时tan(α+β)的值.
解:(1)由已知,得sinβ=sinαcos(α+β)=sinαcosαcosβ-sin2αsinβ, ∴(1+sin2α)sinβ=sinαcosαcosβ. ∴tanβ=![]() =
=![]() =
=![]() . (2)tanβ=
. (2)tanβ=![]() =
=![]() . ∵α∈(0,
. ∵α∈(0,![]() ),∴tanα>0,cotα>0. 而cotα+2tanα≥2
),∴tanα>0,cotα>0. 而cotα+2tanα≥2![]() =2
=2![]() ∴tanβ≤
∴tanβ≤![]() =
=![]() . 当且仅当cotα=2tanα时取“=”,即α=arctan
. 当且仅当cotα=2tanα时取“=”,即α=arctan![]() 时,tanβ达到最大值
时,tanβ达到最大值![]() ,此时tan(α+β)=
,此时tan(α+β)=![]() =
=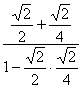 =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目