题目内容
已知A,B,P是双曲线 -
- =1上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率乘积kPA•kPB=3,则双曲线的离心率为
=1上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率乘积kPA•kPB=3,则双曲线的离心率为
- A.

- B.

- C.2
- D.

C
分析:设出点点的坐标,求出斜率,将点的坐标代入方程,两式相减,再结合kPA•kPB=3,即可求得结论.
解答:由题意,设A(x1,y1),P(x2,y2),则B(-x1,-y1)
∴kPA•kPB= ×
× =
=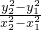
∵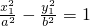 ,
,
∴两式相减可得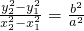
∵kPA•kPB=3,
∴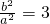
∴
∴e=2
故选C.
点评:本题考查双曲线的方程,考查双曲线的几何性质,属于基础题.
分析:设出点点的坐标,求出斜率,将点的坐标代入方程,两式相减,再结合kPA•kPB=3,即可求得结论.
解答:由题意,设A(x1,y1),P(x2,y2),则B(-x1,-y1)
∴kPA•kPB=
 ×
× =
=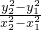
∵
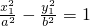 ,
,
∴两式相减可得
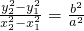
∵kPA•kPB=3,
∴
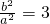
∴

∴e=2
故选C.
点评:本题考查双曲线的方程,考查双曲线的几何性质,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )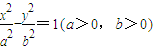 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若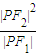 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )