题目内容
设函数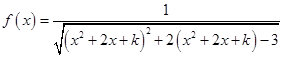 ,其中
,其中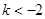 .
.
(1)求函数 的定义域
的定义域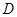 (用区间表示);
(用区间表示);
(2)讨论函数 在
在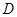 上的单调性;
上的单调性;
(3)若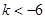 ,求
,求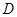 上满足条件
上满足条件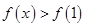 的
的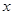 的集合(用区间表示).
的集合(用区间表示).
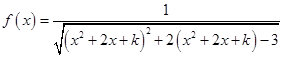 ,其中
,其中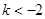 .
.(1)求函数
 的定义域
的定义域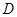 (用区间表示);
(用区间表示);(2)讨论函数
 在
在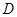 上的单调性;
上的单调性;(3)若
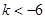 ,求
,求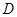 上满足条件
上满足条件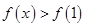 的
的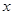 的集合(用区间表示).
的集合(用区间表示).(1)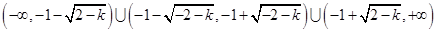 ;
;
(2)单调递增区间为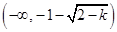 ,
,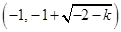 ,
,
递减区间为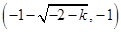 ,
,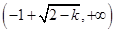 ;
;
(3)
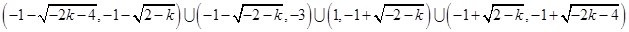 .
.
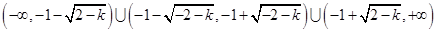 ;
;(2)单调递增区间为
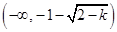 ,
,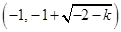 ,
,递减区间为
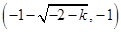 ,
,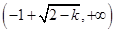 ;
;(3)
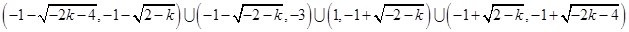 .
.试题分析:(1)由已知条件得到
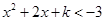 或
或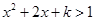 ,对上述两个不等式进行求解,并比较端点值的大小,从而求出函数
,对上述两个不等式进行求解,并比较端点值的大小,从而求出函数 的定义域
的定义域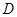 ;(2)求导
;(2)求导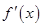 ,并求出方程
,并求出方程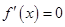 的根,求出不等式
的根,求出不等式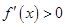 的解集,并与定义域取交集得到函数
的解集,并与定义域取交集得到函数 的单调递增区间,用同样的办法求出函数
的单调递增区间,用同样的办法求出函数 的单调递减区间,但需注意比较各端点值得大小;(3)先求出方程
的单调递减区间,但需注意比较各端点值得大小;(3)先求出方程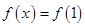 的解,然后结合函数
的解,然后结合函数 的单调性以及函数
的单调性以及函数 的定义域得到不等式
的定义域得到不等式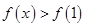 的解集合.
的解集合.试题解析:(1)可知
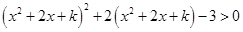 ,
,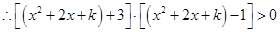 ,
,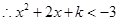 或
或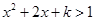 ,
,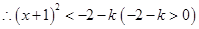 或
或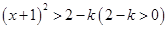 ,
,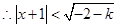 或
或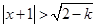 ,
,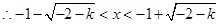 或
或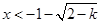 或
或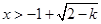 ,
,所以函数
 的定义域
的定义域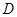 为
为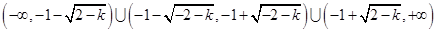 ;
;(2)
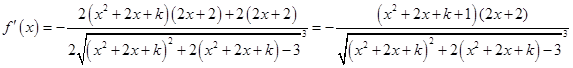 ,
,由
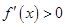 得
得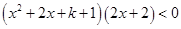 ,即
,即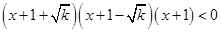 ,
,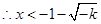 或
或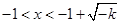 ,结合定义域知
,结合定义域知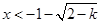 或
或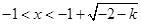 ,
,所以函数
 的单调递增区间为
的单调递增区间为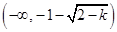 ,
,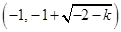 ,
,同理递减区间为
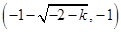 ,
,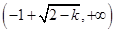 ;
;(3)由
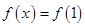 得
得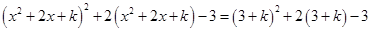 ,
,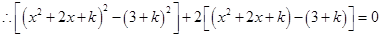 ,
,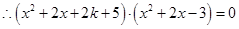 ,
,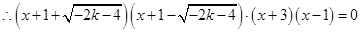 ,
,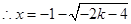 或
或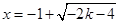 或
或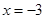 或
或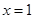 ,
,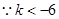 ,
,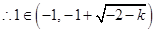 ,
,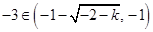 ,
,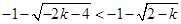 ,
,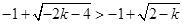 ,
,结合函数
 的单调性知
的单调性知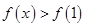 的解集为
的解集为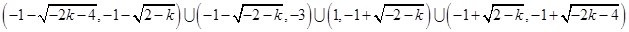 .
.【考点定位】本题以复合函数为载体,考查函数的定义域、单调区间以及不等式的求解,从中渗透了二次不等式的求解,在求定义域时考查了分类讨论思想,以及利用作差法求解不等式的问题,综合性强,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
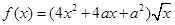 ,其中
,其中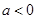 .
.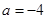 时,求
时,求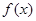 的单调递增区间;
的单调递增区间;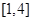 上的最小值为8,求
上的最小值为8,求 的值.
的值.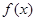 ,
,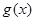 分别是定义在
分别是定义在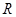 上的奇函数和偶函数,当
上的奇函数和偶函数,当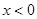 时,
时,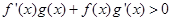 ,且
,且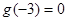 ,则不等式
,则不等式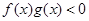 的解集是 ( )
的解集是 ( )



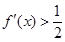 ,则满足
,则满足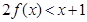 的x的集合为( )
的x的集合为( )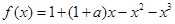 ,其中
,其中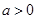
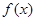 在其定义域上的单调性;
在其定义域上的单调性;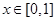 时,求
时,求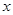 的值.
的值.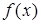 在R上可导,其导函数为
在R上可导,其导函数为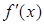 且函数
且函数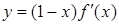 的图像如图所示,则下列结论一定成立的是( )
的图像如图所示,则下列结论一定成立的是( )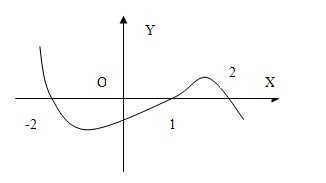
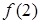 ,极小值是
,极小值是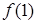
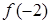 ,极小值是
,极小值是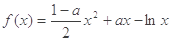 (
( )
) 时,求函数
时,求函数 的极值;(2)当
的极值;(2)当 时,讨论
时,讨论