题目内容
为了研究某高校大学新生学生的视力情况，随机地抽查了该校100名进校学生的视力情况，得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列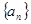
的前四项，后6组的频数从左到右依次是等差数列
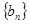的前六项．(Ⅰ)求等比数列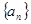的通项公式;
（Ⅱ）求等差数列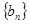的通项公式；(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
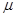的大小.
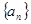的前四项，后6组的频数从左到右依次是等差数列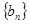的前六项．(Ⅰ)求等比数列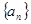的通项公式;（Ⅱ）求等差数列
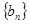的通项公式；(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率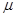的大小.（1）
；（2）
；（3）91%.
；（2）；（3）91%.(I)根据每个区间上的矩形面积为频率，然后频率
总体=频数。
（II）根据（I）中的方法可求数列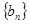的通项公式;
(III)根据（I）（II）可知=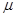
解：（I）由题意知：
，
…2分
∵数列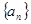是等比数列，∴公比
∴ .……4分
(II) ∵
=13,∴
，…6分
∵数列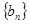是等差数列，∴设数列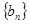公差为
，则得，
∴
＝87，
，
……8分 …10分
(III)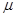=, (或=
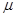)…11分
答:估计该校新生近视率为91%.
总体=频数。（II）根据（I）中的方法可求数列
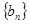的通项公式;(III)根据（I）（II）可知
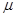=解：（I）由题意知：
， …2分∵数列
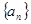是等比数列，∴公比∴ .……4分(II) ∵
=13,∴，…6分∵数列
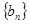是等差数列，∴设数列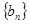公差为，则得，∴
＝87，，……8分 …10分(III)
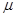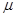=, (或=)…11分答:估计该校新生近视率为91%.
练习册系列答案
名校课堂系列答案
相关题目
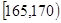
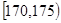
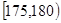
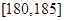
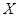为这两名学生来自第3组的人数，求
、
… 
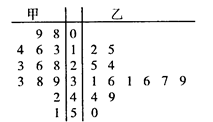
之间满足
，若
恒为0，则
为 .