题目内容
在用数学归纳法证明凸n边形内角和定理时,第一步应验证( )
| A.n=1时成立 | B.n=2时成立 |
| C.n=3时成立 | D.n=4时成立 |
C
解析

练习册系列答案
相关题目
把数列 的各项按顺序排列成如下的三角形状,
的各项按顺序排列成如下的三角形状,
记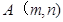 表示第
表示第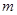 行的第
行的第 个数,若
个数,若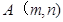 =
=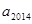 ,则
,则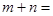 ( )
( )
| A.122 | B.123 | C.124 | D.125 |
下面是一段演绎推理:
如果直线平行于平面,则这条直线平行于平面内的所有直线;
已知直线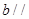 平面
平面 ,直线
,直线 平面
平面 ;
;
所以直线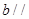 直线
直线 ,在这个推理中( )
,在这个推理中( )
| A.大前提正确,结论错误 |
| B.小前提与结论都是错误的 |
| C.大、小前提正确,只有结论错误 |
| D.大前提错误,结论错误 |
用反证法证明命题“如果你 ,那么
,那么 ”时,假设的内容是
”时,假设的内容是
A.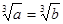 | B. |
C.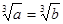 且 且 | D.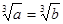 或 或 |
用反证法证明命题“若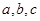 都是正数,则
都是正数,则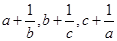 三数中至少有一个不小于
三数中至少有一个不小于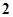 ”,提出的假设是( )
”,提出的假设是( )
A.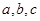 不全是正数 不全是正数 |
B.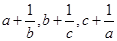 至少有一个小于 至少有一个小于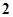 |
C.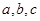 都是负数 都是负数 |
D.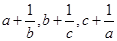 都小于2 都小于2 |
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
| A.假设三个内角都不大于60度 |
| B.假设三个内角都大于60度 |
| C.假设三个内角至多有一个大于60度 |
| D.假设三个内角有两个大于60度 |
下列代数式(其中k∈N*)能被9整除的是( )
| A.6+6·7k | B.2+7k-1 |
| C.2(2+7k+1) | D.3(2+7k) |
 (n≥2),每个数是它下一行左右相邻两数的和,如
(n≥2),每个数是它下一行左右相邻两数的和,如 =
= +
+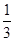 +
+ ,
, +
+ ,则第10行第4个数(从左往右数)为( )
,则第10行第4个数(从左往右数)为( )



