题目内容
已知函数 的反函数为
的反函数为 ,设
,设 的图象上在点
的图象上在点 处的切线在y轴上的截距为
处的切线在y轴上的截距为 ,数列{
,数列{ }满足:
}满足:
(Ⅰ)求数列{ }的通项公式;
}的通项公式;
(Ⅱ)在数列 中,仅
中,仅 最小,求
最小,求 的取值范围;
的取值范围;
(Ⅲ)令函数 数列
数列 满足
满足 ,求证:对一切n≥2的正整数都有
,求证:对一切n≥2的正整数都有
(Ⅰ)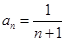 ;(Ⅱ)
;(Ⅱ) 的取值范围为
的取值范围为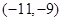 ;(Ⅲ)详见解析
;(Ⅲ)详见解析
解析试题分析:(Ⅰ)将函数 的反函数求出来,可得
的反函数求出来,可得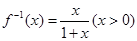 ,
,
再由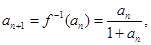 得
得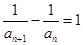
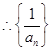 是以2为首项,l为公差的等差数列,由此可得数列{
是以2为首项,l为公差的等差数列,由此可得数列{ }的通项公式
}的通项公式
(Ⅱ)求出函数 的反函数在点
的反函数在点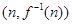 处的切线的截距即得
处的切线的截距即得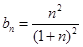
将 ,
, 的通项公式代入
的通项公式代入 得:
得: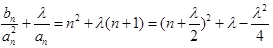
这是一个二次函数,但n只取正整数,画出图象可以看出当对称轴介于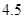 与
与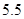 之间的时候,就仅有
之间的时候,就仅有 最小,
最小,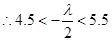 ,解这个不等式即可得
,解这个不等式即可得 的取值范围
的取值范围
(Ⅲ)由题设可得: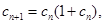 结合待证不等式可看出,可将这个等式两边取倒数,这样可得:
结合待证不等式可看出,可将这个等式两边取倒数,这样可得: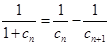 ,从而
,从而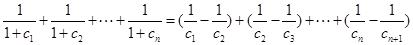
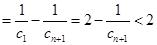
又递推公式可知, 各项为正,所以
各项为正,所以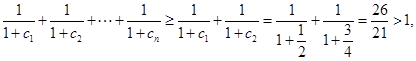
试题解析:(Ⅰ)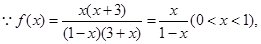
∴函数 的反函数
的反函数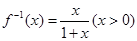
则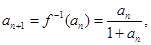 得
得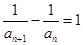
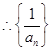 是以2为首项,l为公差的等差数列,故
是以2为首项,l为公差的等差数列,故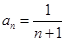 (3分)
(3分)
(Ⅱ)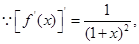
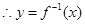 在点
在点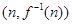 处的切线方程为
处的切线方程为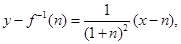 令
令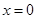 , 得
, 得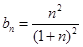
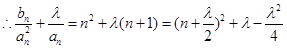 (6分)
(6分)
依题意,仅当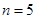 时取得最小值,
时取得最小值,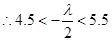 ,解之
,解之
∴ 的取值范围为
的取值范围为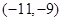 (8分)
(8分)
(Ⅲ)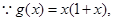 故
故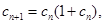
又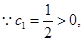 故
故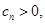
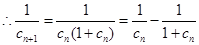 ,
,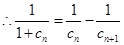
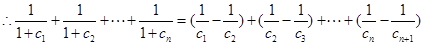
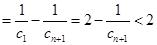
又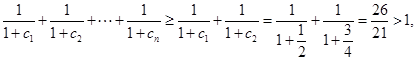
故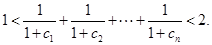 (14分)
(14分)
考点:1、数列与不等式;2、函数的反函数;3、利用导数求切线

练习册系列答案
相关题目
 ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于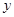 轴.
轴. 的值;
的值; 的极值.
的极值.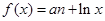 ,其中实数a为常数.
,其中实数a为常数. 的单调区间:
的单调区间: (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值; .
. 的图象在
的图象在 上连续,定义:
上连续,定义: ,
,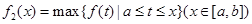 .其中,
.其中, 表示函数
表示函数 上的最小值,
上的最小值, 表示函数
表示函数 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 ,试写出
,试写出 ,
, 的表达式;
的表达式; ,试判断
,试判断 上的“
上的“ ,函数
,函数 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.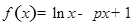 .
.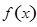 的极值点;
的极值点;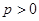 时,若对任意的
时,若对任意的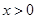 ,恒有
,恒有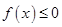 ,求
,求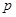 的取值范围;
的取值范围;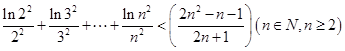 .
. ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴.
轴. 的值;
的值; 的极值.
的极值. 元,则销售量
元,则销售量 (单位:件)与零售价
(单位:件)与零售价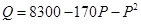 ,问该商品零售价定为多少元时毛利润
,问该商品零售价定为多少元时毛利润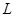 最大,并求出最大毛利润.(毛利润
最大,并求出最大毛利润.(毛利润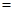 销售收入
销售收入 进货支出)
进货支出) .
. 的单调递减区间;
的单调递减区间;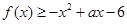 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; 作函数
作函数 图像的切线,求切线方程
图像的切线,求切线方程 在
在 处的切线与
处的切线与 轴平行.
轴平行. 的值和函数
的值和函数 的单调区间;
的单调区间; 的图象与抛物线
的图象与抛物线 恰有三个不同交点,求
恰有三个不同交点,求 的取值范围.
的取值范围.