题目内容
数列{an}的前n项和为Sn,若a1=3,点(Sn,Sn+1)在直线 (n∈N*)上.
(n∈N*)上.
(Ⅰ)求证:数列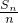 是等差数列;
是等差数列;
(Ⅱ)若数列{bn}满足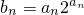 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(Ⅲ)设 ,求证:
,求证: .
.
解:(Ⅰ)∵点(Sn,Sn+1)在直线 (n∈N*)上,
(n∈N*)上,
 ,
,
同除以n+1,则有: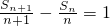
∴数列{ }是以3为首项,1为公差的等差数列.
}是以3为首项,1为公差的等差数列.
(Ⅱ)由(Ⅰ)可知,Sn=n2+2n(n∈N*),∴当n=1时,a1=3,
当n≥2时,an=Sn-Sn-1=2n+1,经检验,当n=1时也成立,
∴an=2n+1(n∈N*).
∵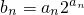 ,∴bn=(2n+1)•22n+1,
,∴bn=(2n+1)•22n+1,
Tn=3•23+5•25++(2n-1)•22n-1+(2n+1)•22n+14Tn
=3•25++(2n-3)22n-1+(2n-1)22n+1+(2n+1)22n+3
解得:Tn= .
.
(Ⅲ)∵ =
=
∴

 .
.
分析:(Ⅰ)由点(Sn,Sn+1)在直线 (n∈N*)上,得
(n∈N*)上,得 ,对此式两边同除以n+1,得到
,对此式两边同除以n+1,得到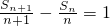 ,可证得结论;
,可证得结论;
(Ⅱ)由(Ⅰ)可知,能求得Sn,根据 ,求出数列{an}的通项公式,代入可求得数列{bn}的通项公式,然后利用错位相减法求得数列{bn}的前n项和Tn;
,求出数列{an}的通项公式,代入可求得数列{bn}的通项公式,然后利用错位相减法求得数列{bn}的前n项和Tn;
(Ⅲ)把(II)求得的结果代入 ,利用分组求和法求得数列{cn}的前n项和,再证明不等式即可.
,利用分组求和法求得数列{cn}的前n项和,再证明不等式即可.
点评:此题是个难题.考查根据数列的递推公式利用构造法求数列的通项公式,及数列的求和问题,题目综合性强,特别是问题(Ⅲ)的设置,数列与不等式恒成立问题结合起来,能有效考查学生的逻辑思维能力和灵活应用知识分析解决问题的能力,体现了转化的思想和分类讨论的思想.
 (n∈N*)上,
(n∈N*)上, ,
,同除以n+1,则有:
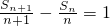
∴数列{
 }是以3为首项,1为公差的等差数列.
}是以3为首项,1为公差的等差数列.(Ⅱ)由(Ⅰ)可知,Sn=n2+2n(n∈N*),∴当n=1时,a1=3,
当n≥2时,an=Sn-Sn-1=2n+1,经检验,当n=1时也成立,
∴an=2n+1(n∈N*).
∵
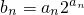 ,∴bn=(2n+1)•22n+1,
,∴bn=(2n+1)•22n+1,Tn=3•23+5•25++(2n-1)•22n-1+(2n+1)•22n+14Tn
=3•25++(2n-3)22n-1+(2n-1)22n+1+(2n+1)22n+3
解得:Tn=
 .
.(Ⅲ)∵
 =
=
∴


 .
.分析:(Ⅰ)由点(Sn,Sn+1)在直线
 (n∈N*)上,得
(n∈N*)上,得 ,对此式两边同除以n+1,得到
,对此式两边同除以n+1,得到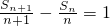 ,可证得结论;
,可证得结论;(Ⅱ)由(Ⅰ)可知,能求得Sn,根据
 ,求出数列{an}的通项公式,代入可求得数列{bn}的通项公式,然后利用错位相减法求得数列{bn}的前n项和Tn;
,求出数列{an}的通项公式,代入可求得数列{bn}的通项公式,然后利用错位相减法求得数列{bn}的前n项和Tn;(Ⅲ)把(II)求得的结果代入
 ,利用分组求和法求得数列{cn}的前n项和,再证明不等式即可.
,利用分组求和法求得数列{cn}的前n项和,再证明不等式即可.点评:此题是个难题.考查根据数列的递推公式利用构造法求数列的通项公式,及数列的求和问题,题目综合性强,特别是问题(Ⅲ)的设置,数列与不等式恒成立问题结合起来,能有效考查学生的逻辑思维能力和灵活应用知识分析解决问题的能力,体现了转化的思想和分类讨论的思想.

练习册系列答案
相关题目