题目内容
已知实数组成的数组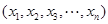 满足条件:
满足条件:
①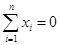 ; ②
; ②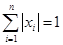 .
.
(Ⅰ) 当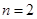 时,求
时,求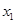 ,
,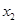 的值;
的值;
(Ⅱ)当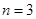 时,求证:
时,求证: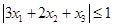 ;
;
(Ⅲ)设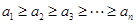 ,且
,且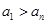
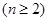 ,求证:
,求证: .
.
【答案】
(1) 或
或 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)列出方程组 求解;(2)应用绝对值不等式
求解;(2)应用绝对值不等式 进行证明;(3)应用绝对值不等式可以证明.
进行证明;(3)应用绝对值不等式可以证明.
试题解析:(Ⅰ)解:
由(1)得 ,再由(2)知
,再由(2)知 ,且
,且 .
.
当 时,
时, .得
.得 ,所以
,所以 2分
2分
当 时,同理得
时,同理得 4分
4分
(Ⅱ)证明:当 时,
时,
由已知 ,
, .
.
所以

 .
9分
.
9分
(Ⅲ)证明:因为 ,且
,且
 .
.
所以

 ,
,
即
 .
11分
.
11分



 )
)

 .
14分.
.
14分.
考点:绝对值不等式.

练习册系列答案
相关题目

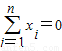 ; ②
; ② .
.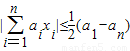 .
.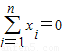 ; ②
; ② .
. .
.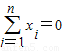 ; ②
; ②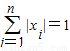 .
.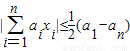 .
.