题目内容
13.2015年上海国际机动车尾气净化及污染控制研讨会在上海召开,大会一致决定,加强对汽车碳排放量的严控,汽车是碳排放量比较大的行业之一,我市规定,从2015年开始,将对二氧化碳排放量超130g/km的轻型汽车进行惩罚性征税.检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km).| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | 100 | 160 |
(Ⅰ)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性;
(Ⅱ)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过130g/km的概率是多少?
分析 (1)由平均数 $\overline{x}$乙=120g/km计算x的值,求出甲品牌二氧化碳排放量的平均数,再由求出甲乙的方差,比较平均数和方差得答案.
(2)用枚举法列出从被检测的5辆甲品牌轻型汽车中任取2辆的所有不同的二氧化碳排放量结果,查出至少有一辆二氧化碳排放量超过130g/km的种数,然后由古典概型概率计算公式求概率;
解答 解:(1)由题可知,$\overline{{x}_{乙}}$=120,∴$\frac{480+x}{5}$=120,
解得 x=120.
又$\overline{{x}_{甲}}$=120,
∴${{s}_{甲}}^{2}$=$\frac{1}{5}$[(80-120)2+(110-120)2+(120-120)2+(140-120)2+(150-120)2]=600,
∴${{s}_{乙}}^{2}$=$\frac{1}{5}$[(100-120)2+(120-120)2+(120-120)2+(100-120)2+(160-120)2]=480,
∵$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$=120,${{s}_{甲}}^{2}$>${{s}_{乙}}^{2}$,
∴乙品牌轻型汽车二氧化碳排放量的稳定性好.
(2)从被检测的5辆甲品牌的轻型汽车中任取2辆,共有10种不同的二氧化碳排放量结果:
(80,110),(80,120),(80,140),(80,150),(110,120),(110,140),
(110,150),(120,140),(120,150),(140,150).
设“至少有一辆二氧化碳排放量超过130g/km”为事件A,则事件A包含以下7种不同的结果:
(80,140),(80,150),(110,140),(110,150),(120,140),(120,150),
(140,150)
∴P(A)=$\frac{7}{10}$=0.7.
答:至少有一辆二氧化碳排放量超过130g/km的概率为0.7;
点评 本题考查了古典概型概率计算公式,训练了利用列举法列举基本事件个数,考查了平均数与方差公式,是基础的计算题.

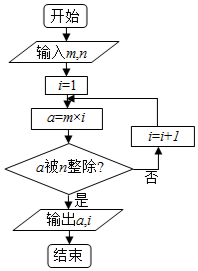 当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )
当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )| A. | 37${C}_{12}^{7}$ | B. | 38${C}_{12}^{8}$ | C. | -33${C}_{12}^{3}$ | D. | -37${C}_{12}^{5}$ |
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
| A. | f(x)=x2|x| | B. | f(x)=-xe|x| | ||
| C. | f(x)=$\left\{\begin{array}{l}{lg(x+1),x≥0}\\{lg(1-x),x<0}\\{\;}\end{array}\right.$ | D. | f(x)=x+sinx |
| A. | $\sqrt{3}$+1 | B. | $\sqrt{2}$+1 | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{2}+1}{2}$ |
| A. | f($\sqrt{2}$)<f(2)<f(3) | B. | f(2)<f(3)<f($\sqrt{2}$) | C. | f(3)<f(2)<f($\sqrt{2}$) | D. | f(3)<f($\sqrt{2}$)<f(2) |