题目内容
函数f(x)=
+
的最小值是
.
| x2+1 |
| x2-4x+8 |
| 13 |
| 13 |
分析:将根式进行配方,将函数转化为两点间的距离关系进行求解即可.
解答:解:f(x)=
+
=
+
,
令P(x,0),A(0,-1),B(2,2),
则PA+PB=
+
,
∴函数f(x)的几何意义是动点P到定点A,B两点距离之和的取值范围,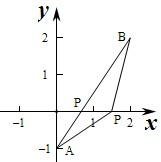
由图象可知,当A,B,P三点共线时,PA+PB的值最小,
此时PA+PB≥AB=
=
=
,
故答案为:
.
| x2+1 |
| x2-4x+8 |
| (x-0)2+(0+1)2 |
| (x-2)2+(0-2)2 |
令P(x,0),A(0,-1),B(2,2),
则PA+PB=
| (x-0)2+(0+1)2 |
| (x-2)2+(0-2)2 |
∴函数f(x)的几何意义是动点P到定点A,B两点距离之和的取值范围,

由图象可知,当A,B,P三点共线时,PA+PB的值最小,
此时PA+PB≥AB=
| (0-2)2+(-1-2)2 |
| 4+9 |
| 13 |
故答案为:
| 13 |
点评:本题主要考查函数的最值的求法,利用根式的特点将代数问题转化为几何问题是解决本题的关键,考查了两点之间线段最短的性质.

练习册系列答案
相关题目