题目内容
设xy<0,x,y∈R,那么下列结论正确的是
- A.|x+y|<|x-y|
- B.|x-y|<|x|+|y|
- C.|x+y|>|x-y|
- D.|x-y|<||x|-|y||
A
因为设xy<0,x,y∈R,那|x+y|<|x-y|显然成立,选项B中,不成立,选项C中,显然不成立,选项D中,应该是|x-y|>||x|-|y||,故选A
因为设xy<0,x,y∈R,那|x+y|<|x-y|显然成立,选项B中,不成立,选项C中,显然不成立,选项D中,应该是|x-y|>||x|-|y||,故选A

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
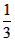 )=1,
)=1,