题目内容
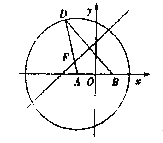
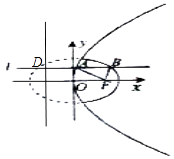
【题目】如图动直线l：y=b与抛物线y2=4x交于点A，与椭圆 
=1交于抛物线右侧的点B，F为抛物线的焦点，则|AF|+|BF|+|AB|的最大值为（ ）
A.
B.
C.2
D.
【答案】D
【解析】解：直线l：y=b与抛物线y2=4x交于点A，F为抛物线的焦点，直线y=b与x=﹣1的交点为D，由抛物线定义，可知AF=AD，|AF|+|BF|+|AB|的最大值，就是BD+BF的最大值，F（1，0），设B（x，b），椭圆 
=1的焦点坐标（1，0）．
可得 
，|AF|+|BF|+|AB|=x+1+ 
=x+1+ 
=x+1+ 
=x+1+ 
=1+ 
+x（1﹣ 
），x∈（0， ]．
当x= 时，1+ +x（1﹣ ）=1+ + （1﹣ ）=2 ，
所以答案是：D．
练习册系列答案
相关题目
