题目内容
设F1,F2为椭圆 的焦点,过F1且垂直于x轴的直线与椭圆交于A,B两点,若△ABF2为锐角三角形,则该椭圆离心率e的取值范围是 .
的焦点,过F1且垂直于x轴的直线与椭圆交于A,B两点,若△ABF2为锐角三角形,则该椭圆离心率e的取值范围是 .
【答案】分析:先依据条件求出AF1的长度,由题意知∠AF2F1 小于45°,由 tan∠AF2F1<1 建立关于a、c的不等式,
转化为关于e的不等式,解此不等式求出离心率e的范围,再结合 0<e<1 得到准确的离心率e的范围.
解答:解:由题意知∠AF2F1 小于45°,故 tan∠AF2F1 ;= <1,即
<1,即  <1,
<1,
b2<2ac,a2-c2<2ac,e2+2e-1>0,∴e> -1,或 e<-1-
-1,或 e<-1- (舍去).
(舍去).
又 0<e<1,故有 -1<e<1,
-1<e<1,
故答案为: -1<e<1.
-1<e<1.
点评:本题考查椭圆的标准方程和简单的性质,利用∠AF2F1 小于45°,tan∠AF2F1<1求出e的范围,将此范围与 0<e<1取交集.
转化为关于e的不等式,解此不等式求出离心率e的范围,再结合 0<e<1 得到准确的离心率e的范围.
解答:解:由题意知∠AF2F1 小于45°,故 tan∠AF2F1 ;=
 <1,即
<1,即  <1,
<1,b2<2ac,a2-c2<2ac,e2+2e-1>0,∴e>
 -1,或 e<-1-
-1,或 e<-1- (舍去).
(舍去).又 0<e<1,故有
 -1<e<1,
-1<e<1,故答案为:
 -1<e<1.
-1<e<1.点评:本题考查椭圆的标准方程和简单的性质,利用∠AF2F1 小于45°,tan∠AF2F1<1求出e的范围,将此范围与 0<e<1取交集.

练习册系列答案
相关题目
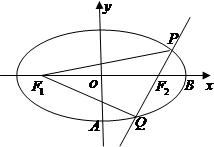 已知椭圆
已知椭圆