题目内容
是否存在最大的正整数m,使得f(n)=(2n+7)•3n+9对任意正整数n都能被m整除?
分析:计算f(1),f(2),f(3)猜测存在m=36,然后直接利用数学归纳法的证明步骤证明即可.
解答:解:f(1)=(2+7)•3+9=36,
f(2)=(2×2+7)•32+9=36×3,
f(3)=(2×3+7)•33+9=36×10,
猜测存在m=36(2分)
①当n=1时,f(1)=(2+7)•3+9=36能被36整除(1分)
②假设n=k时,f(k)=(2k+7)•3k+9能被36整除
当n=k+1时,f(k+1)=[2(k+1)+7)]•3k+1+9
=3[(2k+7)3k+9+(2×3k-9)]+9
=3[(2k+7)3k+9]+6×3k-18
=3[(2k+7)3k+9]+18(3k-1-1)(3分)
∵k∈N*,∴3k-1-1为偶数,18(3k-1-1)能被36整除(2分)
∴f(k+1)=3[(2k+7)3k+9]+18(3k-1-1)能被36整除(1分)
∴n=k+1时,猜测也成立
由①②可知对任意正整数n猜测都成立
故存在m=36(1分)
f(2)=(2×2+7)•32+9=36×3,
f(3)=(2×3+7)•33+9=36×10,
猜测存在m=36(2分)
①当n=1时,f(1)=(2+7)•3+9=36能被36整除(1分)
②假设n=k时,f(k)=(2k+7)•3k+9能被36整除
当n=k+1时,f(k+1)=[2(k+1)+7)]•3k+1+9
=3[(2k+7)3k+9+(2×3k-9)]+9
=3[(2k+7)3k+9]+6×3k-18
=3[(2k+7)3k+9]+18(3k-1-1)(3分)
∵k∈N*,∴3k-1-1为偶数,18(3k-1-1)能被36整除(2分)
∴f(k+1)=3[(2k+7)3k+9]+18(3k-1-1)能被36整除(1分)
∴n=k+1时,猜测也成立
由①②可知对任意正整数n猜测都成立
故存在m=36(1分)
点评:本题考查数学归纳法证明问题的步骤,证明整除问题的方法,注意n=k+1时必须用上假设,考查计算能力.

练习册系列答案
相关题目
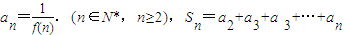 ,问是否存在最大的正整数m,使得对任意的n∈N*均有
,问是否存在最大的正整数m,使得对任意的n∈N*均有 恒成立?若存在,求出m值;若不存在请说明理由.
恒成立?若存在,求出m值;若不存在请说明理由.