题目内容
已知: .(a∈R,a为常数)
.(a∈R,a为常数)
(1)若x∈R,求f(x)的最小正周期;
(2)若f(x)在[ 上的最大值与最小值之和为3,求a的值.
上的最大值与最小值之和为3,求a的值.
解:∵
(1)最小正周期
(2)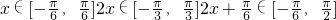
∴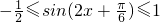
先向右平移 再向下平移1
再向下平移1
即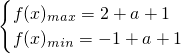 ∴2a+3=3?a=0
∴2a+3=3?a=0
2a+2+1=3,a=0
分析:(1)先利用两角和公式对函数解析式整理,进而根据正弦函数的性质求得函数的最小正周期.
(2)利用(1)中函数的解析式,利用x的范围,确定2x+ 的范围,最后利用正弦函数的单调性求得函数的最大和最小值的表达式,进而二者相加求得a.
的范围,最后利用正弦函数的单调性求得函数的最大和最小值的表达式,进而二者相加求得a.
点评:本题主要考查了三角函数的最值.一般是利用三角函数的值域和定义域来求得三角函数的最值.

(1)最小正周期

(2)
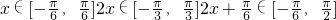
∴
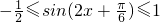
先向右平移
 再向下平移1
再向下平移1即
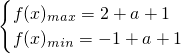 ∴2a+3=3?a=0
∴2a+3=3?a=02a+2+1=3,a=0
分析:(1)先利用两角和公式对函数解析式整理,进而根据正弦函数的性质求得函数的最小正周期.
(2)利用(1)中函数的解析式,利用x的范围,确定2x+
 的范围,最后利用正弦函数的单调性求得函数的最大和最小值的表达式,进而二者相加求得a.
的范围,最后利用正弦函数的单调性求得函数的最大和最小值的表达式,进而二者相加求得a.点评:本题主要考查了三角函数的最值.一般是利用三角函数的值域和定义域来求得三角函数的最值.

练习册系列答案
相关题目
已知x∈R,a∈R,a为常数,且f(x+a)=
,则函数f(x)必有一周期为( )
| 1+f(x) |
| 1-f(x) |
| A、2a | B、3a | C、4a | D、5a |
 .(a∈R,a为常数)
.(a∈R,a为常数) 上的最大值与最小值之和为3,求a的值.
上的最大值与最小值之和为3,求a的值. .(a∈R,a为常数)
.(a∈R,a为常数) 上的最大值与最小值之和为3,求a的值.
上的最大值与最小值之和为3,求a的值.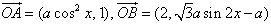 ,f(x)=
,f(x)=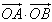 ,
,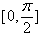 时,f(x)的最大值为5,求a的值;
时,f(x)的最大值为5,求a的值; 上恒成立,求实数m的取值范围。
上恒成立,求实数m的取值范围。