题目内容
已知各项均为正数的数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,满足a1=1, ,其中p为常数.
,其中p为常数.(1)求p的值及数列{an}的通项公式;
(2)①是否存在正整数n,m,k(n<m<k),使得an,am,ak成等差数列?若存在,指出n,m,k的关系;若不存在,请说明理由;
②若对于任意的正整数n,都有an,2xan+1,2yan+2成等差数列,求出实数x,y的值.
【答案】分析:(1)令n=1,代入Tn,求出p的可能取值,经过验证,确定最终的值2.利用an与Sn,an2与Tn的关系,转化,寻求{an}的性质,根据性质求通项.
(2)①假设存在n,m,k(n<m<k),列出关系式,探讨有无解或关系②转换成恒成立问题,注意a=1(a≠0)的使用.
解答:解:(1)当n=1时,Tn=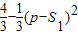 ,即1=
,即1=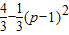 ,∴p=0或p=2
,∴p=0或p=2
当p=0时,Tn=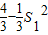 .将n=2代入,得1+a22=
.将n=2代入,得1+a22=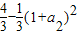 .
.
∴a2=0,或∴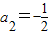 与an>0矛盾.∴p≠0
与an>0矛盾.∴p≠0
当p=2时,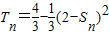 ①
①
将n=2代入,得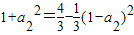 ∴a2=
∴a2= ,a2=
,a2= a1
a1
由①得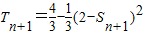 ②
②
②-①得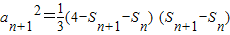
即3an+12=(4-Sn+1-Sn)an+1
则3an+1=4-Sn+1-Sn ③
则 3an+2=4-Sn+2-Sn+1 ④
④-③,得3an+2-3an+1=-an+2-an+1
an+2= an+1,又a2=
an+1,又a2= a1
a1
∴{an}是等比数列,通项公式an=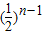 .
.
(2)①假设存在正整数n,m,k(n<m<k),使得an,am,ak成等差数列,则
2am=an+ak,即2×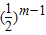 =
=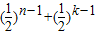
两边同除以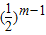 得:2=
得:2=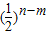 +
+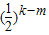 ⑤
⑤
由已知n-m≤-1,∴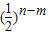 ≥2,且
≥2,且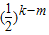 >0
>0
∴⑤式不成立.从而不存在满足条件的n,m,k.
②若对于任意的正整数n,都有an,2xan+1,2yan+2成等差数列
则2x+1an+1=an+2yan+2,根据通项公式,得2x-n+1=21-n+2y-n-1,
两边同除以21-n,得2x=1+2y-2,∴x=1,y=2.
点评:本题考查等比数列的定义,性质,通项公式求解,考查转化能力,分析解决问题能力,计算能力,反证法的运用能力.是难题.
(2)①假设存在n,m,k(n<m<k),列出关系式,探讨有无解或关系②转换成恒成立问题,注意a=1(a≠0)的使用.
解答:解:(1)当n=1时,Tn=
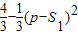 ,即1=
,即1=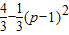 ,∴p=0或p=2
,∴p=0或p=2当p=0时,Tn=
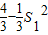 .将n=2代入,得1+a22=
.将n=2代入,得1+a22=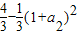 .
.∴a2=0,或∴
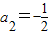 与an>0矛盾.∴p≠0
与an>0矛盾.∴p≠0当p=2时,
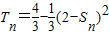 ①
①将n=2代入,得
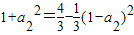 ∴a2=
∴a2= ,a2=
,a2= a1
a1由①得
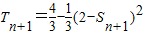 ②
②②-①得
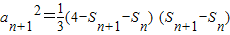
即3an+12=(4-Sn+1-Sn)an+1
则3an+1=4-Sn+1-Sn ③
则 3an+2=4-Sn+2-Sn+1 ④
④-③,得3an+2-3an+1=-an+2-an+1
an+2=
 an+1,又a2=
an+1,又a2= a1
a1∴{an}是等比数列,通项公式an=
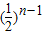 .
.(2)①假设存在正整数n,m,k(n<m<k),使得an,am,ak成等差数列,则
2am=an+ak,即2×
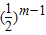 =
=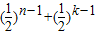
两边同除以
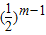 得:2=
得:2=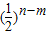 +
+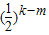 ⑤
⑤由已知n-m≤-1,∴
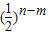 ≥2,且
≥2,且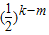 >0
>0∴⑤式不成立.从而不存在满足条件的n,m,k.
②若对于任意的正整数n,都有an,2xan+1,2yan+2成等差数列
则2x+1an+1=an+2yan+2,根据通项公式,得2x-n+1=21-n+2y-n-1,
两边同除以21-n,得2x=1+2y-2,∴x=1,y=2.
点评:本题考查等比数列的定义,性质,通项公式求解,考查转化能力,分析解决问题能力,计算能力,反证法的运用能力.是难题.

练习册系列答案
相关题目
 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明.