Question

已知直线l:3x+y-6=0和圆心为C的圆x²+y²-2y-4=0,判断直线l与圆的位置关系,如果相交,求出它们的交点坐标.

Answer 1

解答:解法一:由直线l:3x+y-6=0和圆x²+y²-2y-4=0的方程得

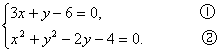
消去y,得x²-3x+2=0.

因为Δ=(-3)²-4×1×2=1＞0,所以直线l与圆相交,有两个公共点.

由x²-3x+2=0,得x₁=2,x₂=1.

把x₁=2代入方程①,得y₁=0;把x₂=1代入方程①,得y₂=3.

所以直线l与圆相交有两个公共点,它们的坐标分别是(2,0)和(1,3).

解法二:圆x²+y²-2y-4=0的方程可化为x²+(y-1)²=5,其圆心C的坐标为(0,1),半径长为5,圆心C到直线l的距离d==＜.

所以直线l与圆相交,有两个公共点.(以后同解法一)

点评:比较两种解法,我们可以看出,几何法判断要比代数法判断快得多,但是若要求交点,仍须联立方程组求解.