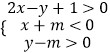Question

【题目】设函数 的定义域为集合 ，函数 的定义域为集合 .
（1）若 ，求实数 的取值范围；
（2）若 ，求实数 的取值范围.

Answer 1

【答案】
（1）解：可知集合 ，集合

若 ，则 ，即 ；

故实数 的取值范围是

（2）解：若 ，则 ，故实数 的取值范围是
【解析】(1)利用真数大于零求出集合A的解集，再利用分母不为零被开方数大于等于零求出集合B，结合子集的定义求出m的取值范围。(2)根据题意结合交集的运算性质即可求出结果。
【考点精析】解答此题的关键在于理解子集与真子集的相关知识，掌握任何一个集合是它本身的子集；n个元素的子集有2n个,n个元素的真子集有2n －1个,n个元素的非空真子集有2n－2个，以及对集合的交集运算的理解，了解交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立．