题目内容
若集合M={y|y=2x,x∈R}, ,则M∩P=
,则M∩P=
- A.{y|y>1}
- B.{y|y≥1}
- C.{y|y>0}
- D.{y|y≥0}
C
分析:根据集合M={y|y=2x,x∈R}, 知M={y|y>0},P={y|y>0},在根据交集的定义即可求解
知M={y|y>0},P={y|y>0},在根据交集的定义即可求解
解答:∵M={y|y=2x,x∈R},
∴M={y|y>0},P={y|y≥0}
∴M∩P={y|y>0}
故选C
点评:本题以集合的交集运算为依托,考查了函数的值域的求法,属于基础题.
分析:根据集合M={y|y=2x,x∈R},
 知M={y|y>0},P={y|y>0},在根据交集的定义即可求解
知M={y|y>0},P={y|y>0},在根据交集的定义即可求解解答:∵M={y|y=2x,x∈R},

∴M={y|y>0},P={y|y≥0}
∴M∩P={y|y>0}
故选C
点评:本题以集合的交集运算为依托,考查了函数的值域的求法,属于基础题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
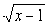 },则M∩P等于 ( )
},则M∩P等于 ( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( )