题目内容
13.在△ABC中,若a=$\sqrt{3}$,b=$\sqrt{7}$,∠B=$\frac{5π}{6}$,则边c=1.分析 直接利用余弦定理列出方程求解即可.
解答 解:在△ABC中,若a=$\sqrt{3}$,b=$\sqrt{7}$,∠B=$\frac{5π}{6}$,
由余弦定理可得:b2=a2+c2-2accosB,
即7=3+c2+2$\sqrt{3}$•$\frac{\sqrt{3}}{2}$c.即c2+3c-4=0,解得c=1或c=-4(舍去)
故答案为:1.
点评 本题考查三角形的解法,余弦定理的应用,考查计算能力.

练习册系列答案
相关题目
4.已知集合A={1,3,4,5},集合B={x∈Z|x2-4x-5<0},则A∩B的子集个数为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
18.执行如图所示的程序框图,则输出的结果为( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
2.已知函数$f(x)=\left\{\begin{array}{l}{log_2}x,x≥1\\ f({2x}),0<x<1.\end{array}\right.$则$f[{{{({\frac{1}{2}})}^{\frac{1}{2}}}}]$=( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
18.i是虚数单位,复数$\frac{4-3i}{2+i}$=( )
| A. | -1-2i | B. | 1+2i | C. | -1+2i | D. | 1-2i |
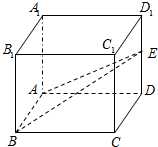 在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).
在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).