题目内容
(本题满分14分)设抛物线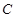 的方程为
的方程为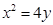 ,
,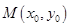 为直线
为直线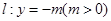 上任意一点,过点
上任意一点,过点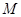 作抛物线
作抛物线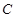 的两条切线
的两条切线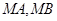 ,切点分别为
,切点分别为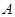 ,
,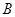 .
.
(1)当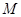 的坐标为
的坐标为 时,求过
时,求过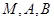 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线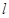 与此圆的位置关系;
与此圆的位置关系;
(2)求证:直线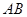 恒过定点
恒过定点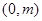 .
.
解:(1)当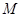 的坐标为
的坐标为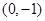 时,设过
时,设过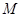 点的切线方程为
点的切线方程为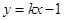 ,代入
,代入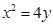 ,整理得
,整理得 ,
,
令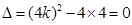 ,解得
,解得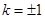 ,
,
代入方程得 ,故得
,故得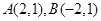 , .................2分
, .................2分
因为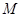 到
到 的中点
的中点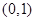 的距离为
的距离为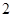 ,
,
从而过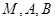 三点的圆的方程为
三点的圆的方程为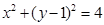 .
.
易知此圆与直线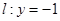 相切.
..................4分
相切.
..................4分
(2)证法一:设切点分别为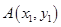 ,
,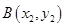 ,过抛物线上点
,过抛物线上点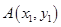 的切线方程为
的切线方程为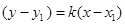 ,代入
,代入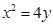 ,整理得
,整理得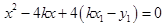
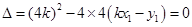 ,又因为
,又因为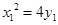 ,所以
,所以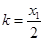 ................6分
................6分
从而过抛物线上点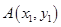 的切线方程为
的切线方程为 即
即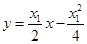
又切线过点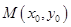 ,所以得
,所以得 ① 即
① 即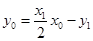 ....8分
....8分
同理可得过点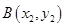 的切线为
的切线为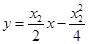 ,
,
又切线过点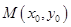 ,所以得
,所以得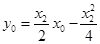 ② ....10分
② ....10分
即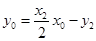 .................6分
.................6分
即点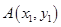 ,
,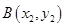 均满足
均满足 即
即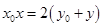 ,故直线
,故直线 的方程为
的方程为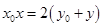 .........................................12分
.........................................12分
又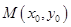 为直线
为直线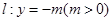 上任意一点,故
上任意一点,故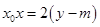 对任意
对任意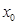 成立,所以
成立,所以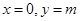 ,从而直线
,从而直线 恒过定点
恒过定点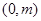 ..................14分
..................14分
证法二:设过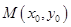 的抛物线的切线方程为
的抛物线的切线方程为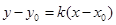
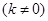 ,代入
,代入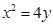 ,消去
,消去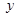 ,得
,得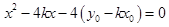
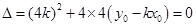 即:
即: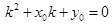 .................6分
.................6分
从而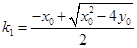 ,
,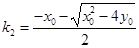 此时
此时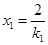 ,
,
所以切点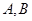 的坐标分别为
的坐标分别为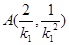 ,
,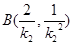 .................8分
.................8分
因为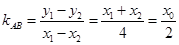 ,
, ,
,
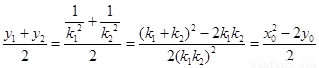 ,
,
所以 的中点坐标为
的中点坐标为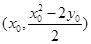 ....................................11分
....................................11分
故直线 的方程为
的方程为 ,即
,即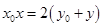 ...........12分
...........12分
又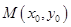 为直线
为直线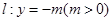 上任意一点,故
上任意一点,故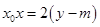 对任意
对任意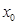 成立,所以
成立,所以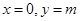 ,从而直线
,从而直线 恒过定点
恒过定点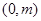 ..................14分
..................14分
证法三:由已知得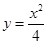 ,求导得
,求导得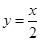 ,切点分别为
,切点分别为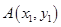 ,
,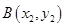 ,故过点
,故过点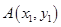 的切线斜率为
的切线斜率为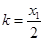 ,从而切线方程为
,从而切线方程为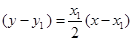 即
即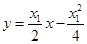
...............................................................7分
又切线过点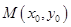 ,所以得
,所以得 ① 即
① 即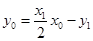 ........8分
........8分
同理可得过点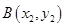 的切线为
的切线为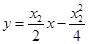 ,
,
又切线过点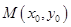 ,所以得
,所以得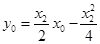 ② 即
② 即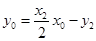 ........10分
........10分
即点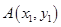 ,
,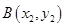 均满足
均满足 即
即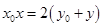 ,故直线
,故直线 的方程为
的方程为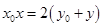 .................12分
.................12分
又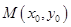 为直线
为直线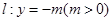 上任意一点,故
上任意一点,故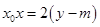 对任意
对任意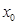 成立,所以
成立,所以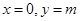 ,从而直线
,从而直线 恒过定点
恒过定点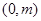 ..................14分
..................14分
【解析】略

 阅读快车系列答案
阅读快车系列答案 的左、右焦点分别为F1与
的左、右焦点分别为F1与 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 满足
满足 ”
” 是集合M中的元素;
是集合M中的元素;
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。  .
. ,求函数
,求函数 的极值;
的极值; ,试确定
,试确定 的单调性;
的单调性; ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.