题目内容
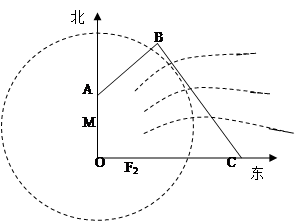
(满分16分)如图:为保护河上古桥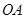 ,规划建一座新桥
,规划建一座新桥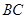 ,同时设立一个圆形保护区,规划要求,新桥
,同时设立一个圆形保护区,规划要求,新桥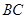 与河岸
与河岸 垂直;保护区的边界为圆心
垂直;保护区的边界为圆心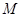 在线段
在线段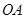 上并与
上并与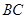 相切的圆,且古桥两端
相切的圆,且古桥两端 和
和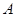 到该圆上任一点的距离均不少于80
到该圆上任一点的距离均不少于80 ,经测量,点
,经测量,点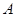 位于点
位于点 正北方向60
正北方向60 处,点
处,点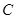 位于点
位于点 正东方向170
正东方向170 处,(
处,(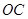 为河岸),
为河岸),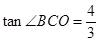 .
.
(1)求新桥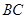 的长;
的长;
(2)当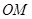 多长时,圆形保护区的面积最大?
多长时,圆形保护区的面积最大?
(1) ;(2)
;(2)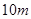 .
.
解析试题分析:本题是应用题,我们可用解析法来解决,为此以 为原点,以向东,向北为坐标轴建立直角坐标系.(1)
为原点,以向东,向北为坐标轴建立直角坐标系.(1) 点坐标炎
点坐标炎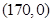 ,
,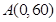 ,因此要求
,因此要求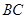 的长,就要求得
的长,就要求得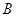 点坐标,已知
点坐标,已知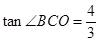 说明直线
说明直线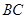 斜率为
斜率为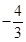 ,这样直线
,这样直线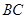 方程可立即写出,又
方程可立即写出,又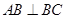 ,故
,故 斜率也能得出,这样
斜率也能得出,这样 方程已知,两条直线的交点
方程已知,两条直线的交点 的坐标随之而得;(2)实质就是圆半径最大,即线段
的坐标随之而得;(2)实质就是圆半径最大,即线段 上哪个点到直线
上哪个点到直线 的距离最大,为此设
的距离最大,为此设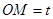 ,由
,由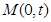 ,圆半径
,圆半径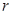 是圆心
是圆心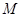 到直线
到直线 的距离,而求它的最大值,要考虑条件古桥两端
的距离,而求它的最大值,要考虑条件古桥两端 和
和 到该圆上任一点的距离均不少于80
到该圆上任一点的距离均不少于80 ,列出不等式组,可求得
,列出不等式组,可求得 的范围,进而求得最大值.当然本题如果用解三角形的知识也可以解决.
的范围,进而求得最大值.当然本题如果用解三角形的知识也可以解决.
试题解析: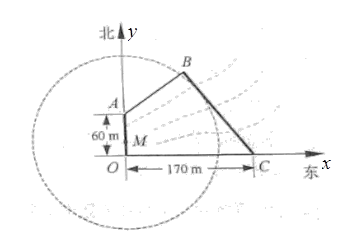
(1)如图,以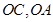 为
为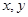 轴建立直角坐标系,则
轴建立直角坐标系,则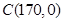 ,
,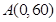 ,由题意
,由题意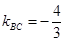 ,直线
,直线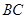 方程为
方程为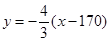 .又
.又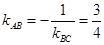 ,故直线
,故直线 方程为
方程为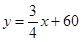 ,由
,由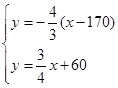 ,解得
,解得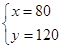 ,即
,即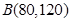 ,所以
,所以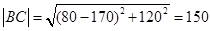
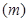 ;
;
(2)设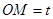 ,即
,即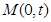
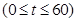 ,由(1)直线
,由(1)直线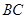 的一般方程为
的一般方程为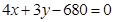 ,圆
,圆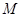 的半径为
的半径为 ,由题意要求
,由题意要求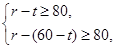 ,由于
,由于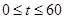 ,因此
,因此
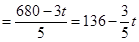 ,∴
,∴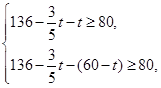 ∴
∴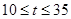 ,所以当
,所以当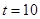 时,
时,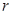 取得最大值
取得最大值 ,此时圆面积最大.
,此时圆面积最大.
【考点】解析几何的应用,直线方程,直线交点坐标,两点间的距离,点到直线的距离,直线与圆的位置关系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
设椭圆C1和抛物线C2的焦点均在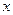 轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
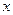 | 3 | -2 | 4 | 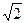 |
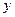 | 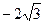 | 0 | -4 | 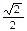 |
(1)求曲线C1,C2的标准方程;
(2)设直线
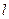 与椭圆C1交于不同两点M、N,且
与椭圆C1交于不同两点M、N,且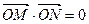 。请问是否存在直线
。请问是否存在直线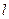 过抛物线C2的焦点F?若存在,求出直线
过抛物线C2的焦点F?若存在,求出直线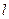 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. 
 ,第二次掷出的点数为
,第二次掷出的点数为 .试就方程组
.试就方程组 (※)解答下列问题:
(※)解答下列问题:
 上的圆的方程.
上的圆的方程. 中,顶点
中,顶点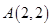 ,边
,边 上的中线
上的中线 所在直线的方程是
所在直线的方程是 ,边
,边 上高
上高 所在直线的方程是
所在直线的方程是 .
. 、C的坐标; (2)求
、C的坐标; (2)求 相切且在两坐标轴上截距相等的直线方程 。
相切且在两坐标轴上截距相等的直线方程 。 ,直线
,直线 与
与 关于直线
关于直线 对称,则直线
对称,则直线