题目内容
在△ABC中,A(cosx,cos2x),B(-
sinx,-cosx),C(λ,1),0≤x≤π,若△ABC的重心在y轴负半轴上,求实数λ的取值范围.
| 3 |
△ABC的重心G在y轴的负半轴上.
则
=0,且
<0,0≤x≤π
所以 2cos2x-1-cosx+1<0,即cosx(2cosx-1)<0,0<cosx<
,故
<x<
∴λ=
sinx-cosx=2(
sinx-
cosx)=2sin(x-
)
∵
<x<
,
<x-
<
π,
<sin(x-
)<
,1<2sin(x-
)<
故 1<λ<
,
λ的取值范围是(1,
).
则
cosx-
| ||
| 3 |
| cos2x-cosx+1 |
| 3 |
所以 2cos2x-1-cosx+1<0,即cosx(2cosx-1)<0,0<cosx<
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴λ=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| 3 |
故 1<λ<
| 3 |
λ的取值范围是(1,
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
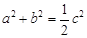 .则直线
.则直线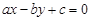 被圆
被圆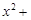
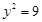 所截得的弦长为 .
所截得的弦长为 .