题目内容
已知函数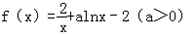 .
.
(1)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求函数y=f(x)的单调区间;
(2)若对于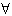 x∈(0,+∞)都有f(x)>2(a﹣1)成立,试求a的取值范围;
x∈(0,+∞)都有f(x)>2(a﹣1)成立,试求a的取值范围;
(3)记g(x)=f(x)+x﹣b(b∈R).当a=1时,函数g(x)在区间[e﹣1,e]上有两个零点,求实数b的取值范围.
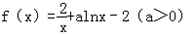 .
.(1)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求函数y=f(x)的单调区间;
(2)若对于
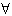 x∈(0,+∞)都有f(x)>2(a﹣1)成立,试求a的取值范围;
x∈(0,+∞)都有f(x)>2(a﹣1)成立,试求a的取值范围;(3)记g(x)=f(x)+x﹣b(b∈R).当a=1时,函数g(x)在区间[e﹣1,e]上有两个零点,求实数b的取值范围.
解:(1)直线y=x+2的斜率为1,函数f(x)的定义域为(0,+∞),
因为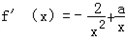 ,
,
所以,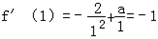 ,
,
所以,a=1.
所以,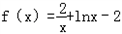 ,
,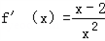 .
.
由f'(x)>0解得x>2;
由f'(x)<0,解得 0<x<2.
所以f(x)的单调增区间是(2,+∞),单调减区间是(0,2).
(2)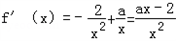 ,
,
由f'(x)>0解得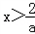 ;
;
由f'(x)<0解得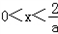 .
.
所以,f(x)在区间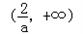 上单调递增,在区间
上单调递增,在区间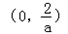 上单调递减.
上单调递减.
所以,当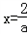 时,函数f(x)取得最小值,
时,函数f(x)取得最小值,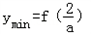 .
.
因为对于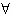 x∈(0,+∞)都有f(x)>2(a﹣1)成立,
x∈(0,+∞)都有f(x)>2(a﹣1)成立,
所以,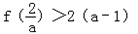 即可. 则
即可. 则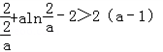 .
.
由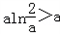 解得
解得 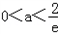 .
.
所以,a的取值范围是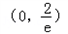 .
.
(3) 依题得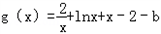 ,则
,则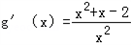 .
.
由g'(x)>0解得 x>1;
由g'(x)<0解得 0<x<1.
所以函数g(x)在区间(0,1)为减函数,在区间(1,+∞)为增函数.
又因为函数g(x)在区间[e﹣1,e]上有两个零点,所以
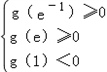 ,
,
解得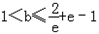 .
.
所以,b的取值范围是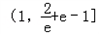 .
.
因为
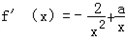 ,
,所以,
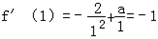 ,
,所以,a=1.
所以,
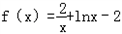 ,
,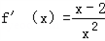 .
. 由f'(x)>0解得x>2;
由f'(x)<0,解得 0<x<2.
所以f(x)的单调增区间是(2,+∞),单调减区间是(0,2).
(2)
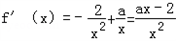 ,
,由f'(x)>0解得
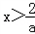 ;
; 由f'(x)<0解得
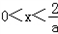 .
.所以,f(x)在区间
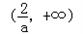 上单调递增,在区间
上单调递增,在区间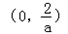 上单调递减.
上单调递减.所以,当
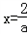 时,函数f(x)取得最小值,
时,函数f(x)取得最小值,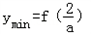 .
.因为对于
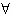 x∈(0,+∞)都有f(x)>2(a﹣1)成立,
x∈(0,+∞)都有f(x)>2(a﹣1)成立,所以,
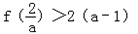 即可. 则
即可. 则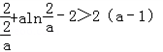 .
. 由
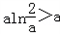 解得
解得 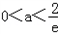 .
.所以,a的取值范围是
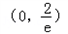 .
.(3) 依题得
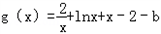 ,则
,则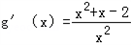 .
.由g'(x)>0解得 x>1;
由g'(x)<0解得 0<x<1.
所以函数g(x)在区间(0,1)为减函数,在区间(1,+∞)为增函数.
又因为函数g(x)在区间[e﹣1,e]上有两个零点,所以
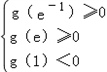 ,
,解得
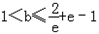 .
. 所以,b的取值范围是
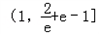 .
.
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 -2lnx、
-2lnx、 -2lnx、
-2lnx、 -2lnx、
-2lnx、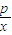 -2lnx、
-2lnx、