题目内容
抛物线y=-x2+4上存在两点关于直线y=kx+3对称,则k的取值范围是________.
k<- 或k>
或k>
分析:设两对称点为A(x1,y1),B(x2,y2),由条件可设AB方程为:y=- x+m,与抛物线方程y=-x2+4消去y得关于x的一元二次方程,则△>0①,由韦达定理可表示AB中点横坐标,代入y=kx+3得其纵坐标,再代入AB方程得m与k的方程
x+m,与抛物线方程y=-x2+4消去y得关于x的一元二次方程,则△>0①,由韦达定理可表示AB中点横坐标,代入y=kx+3得其纵坐标,再代入AB方程得m与k的方程 =-
=- +m②,联立①②即可求得k的取值范围.
+m②,联立①②即可求得k的取值范围.
解答:设两对称点为A(x1,y1),B(x2,y2),则直线AB与直线y=kx+3对称,
易知k≠0,设AB方程为:y=- x+m,
x+m,
由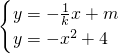 得
得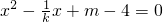 ,则△=
,则△= 0①,
0①,
x1+x2= ,则AB中点横坐标为
,则AB中点横坐标为 ,代入y=kx+3得y=k•
,代入y=kx+3得y=k• +3=
+3= ,所以AB中点坐标为(
,所以AB中点坐标为( ,
, ),
),
又中点在直线AB上,所以 =-
=- •
• +m,即
+m,即 =-
=- +m②,
+m②,
由②得m=( +
+ ),代入①解得k<-
),代入①解得k<- 或k<-
或k<- ,
,
所以k的取值范围为:k<- 或kk>\frac{\sqrt{2}}{2}
或kk>\frac{\sqrt{2}}{2}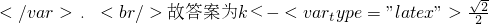 或k>\frac{\sqrt{2}}{2}
或k>\frac{\sqrt{2}}{2}
点评:本题考查直线与圆锥曲线的位置关系,考查轴对称问题,本题采用“方程、不等式”法,解决本题的关键是用数学式子充分刻画条件:两点关于直线对称.
 或k>
或k>
分析:设两对称点为A(x1,y1),B(x2,y2),由条件可设AB方程为:y=-
 x+m,与抛物线方程y=-x2+4消去y得关于x的一元二次方程,则△>0①,由韦达定理可表示AB中点横坐标,代入y=kx+3得其纵坐标,再代入AB方程得m与k的方程
x+m,与抛物线方程y=-x2+4消去y得关于x的一元二次方程,则△>0①,由韦达定理可表示AB中点横坐标,代入y=kx+3得其纵坐标,再代入AB方程得m与k的方程 =-
=- +m②,联立①②即可求得k的取值范围.
+m②,联立①②即可求得k的取值范围.解答:设两对称点为A(x1,y1),B(x2,y2),则直线AB与直线y=kx+3对称,
易知k≠0,设AB方程为:y=-
 x+m,
x+m,由
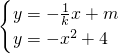 得
得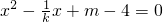 ,则△=
,则△= 0①,
0①,x1+x2=
 ,则AB中点横坐标为
,则AB中点横坐标为 ,代入y=kx+3得y=k•
,代入y=kx+3得y=k• +3=
+3= ,所以AB中点坐标为(
,所以AB中点坐标为( ,
, ),
),又中点在直线AB上,所以
 =-
=- •
• +m,即
+m,即 =-
=- +m②,
+m②,由②得m=(
 +
+ ),代入①解得k<-
),代入①解得k<- 或k<-
或k<- ,
,所以k的取值范围为:k<-
 或kk>\frac{\sqrt{2}}{2}
或kk>\frac{\sqrt{2}}{2}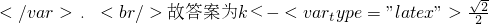 或k>\frac{\sqrt{2}}{2}
或k>\frac{\sqrt{2}}{2}点评:本题考查直线与圆锥曲线的位置关系,考查轴对称问题,本题采用“方程、不等式”法,解决本题的关键是用数学式子充分刻画条件:两点关于直线对称.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
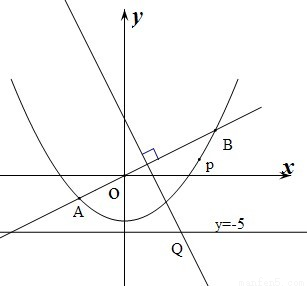
 x与抛物线y=
x与抛物线y= x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.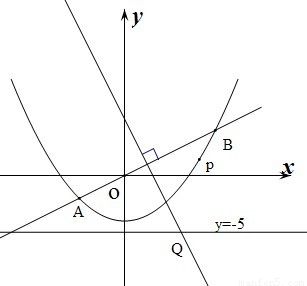
 x与抛物线y=
x与抛物线y= x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.