题目内容
已知函数f（x）=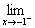
（1）讨论f（x）在点x=－1，0，1处的连续性；
（2）求f（x）的连续区间.
解：（1）f（x）=3，
f（x）=－1，
所以
f（x）不存在.
所以f（x）在x=－1处不连续.
但
f（x）=f（－1）=－1，
f（x）≠f（－1），
所以f（x）在x=－1处右连续，左不连续.
f（x）=3=f（1），
f（x）不存在.
所以
f（x）不存在.
所以f（x）在x=1处不连续，但左连续，右不连续.
又
f（x）=f（0）=0，所以f（x）在x=0处连续.
（2）f（x）中，区间（－∞，－1），［－1，1］，（1，5］上的三个函数都是初等函数，
因此f（x）除不连续点x=±1外，再也无不连续点，所以f（x）的连续区间是（－∞，－1），［－1，1］和（1，5］.
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|