题目内容
连续抛掷两颗骰子,设第一颗点数为m,第二颗点数为n,则求:
(1)m+n=7的概率;(2)m=n的概率;(3)点P(m,n)在圆x2+y2=16内的概率.
解:共有6×6=36个基本事件,
(1)记“m+n=7”为事件A,则A包含6个基本事件,,(1,6),(2,5),(3,4),(4,3),(5,2),(6,1).
故P(A)=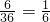 ;
;
(2)记“m=n”为事件B,则B包含6个基本事件,(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),故P(B)=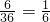 ;
;
(3)记“点P(m,n)在圆x2+y2=16内”为事件C,则C包含8个基本事件,(1,1),(1,2),(1,3),
(2,1)(2,2),(2,3),(3,1),(3,2). 故P(C)= .
.
分析:共有6×6=36个基本事件,(1)记“m+n=7”为事件A,则A包含6个基本事件,故P(A)=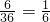 .
.
(2)记“m=n”为事件B,则B包含6个基本事件,故P(B)=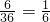 .
.
(3)记“点P(m,n)在圆x2+y2=16内”为事件C,则C包含8个基本事件,故P(C)= .
.
点评:本题考查求等可能事件的概率的方法,关键是求出某事件所包含的基本事件的个数.
(1)记“m+n=7”为事件A,则A包含6个基本事件,,(1,6),(2,5),(3,4),(4,3),(5,2),(6,1).
故P(A)=
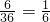 ;
;(2)记“m=n”为事件B,则B包含6个基本事件,(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),故P(B)=
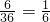 ;
;(3)记“点P(m,n)在圆x2+y2=16内”为事件C,则C包含8个基本事件,(1,1),(1,2),(1,3),
(2,1)(2,2),(2,3),(3,1),(3,2). 故P(C)=
 .
.分析:共有6×6=36个基本事件,(1)记“m+n=7”为事件A,则A包含6个基本事件,故P(A)=
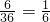 .
.(2)记“m=n”为事件B,则B包含6个基本事件,故P(B)=
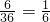 .
.(3)记“点P(m,n)在圆x2+y2=16内”为事件C,则C包含8个基本事件,故P(C)=
 .
.点评:本题考查求等可能事件的概率的方法,关键是求出某事件所包含的基本事件的个数.

练习册系列答案
相关题目