题目内容

【题目】如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且， .

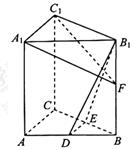
求证：（1）直线DE平面A1C1F；

（2）平面B1DE⊥平面A1C1F.

【答案】（1）详见解析（2）详见解析

【解析】试题（1）利用线面平行判定定理证明线面平行，而线线平行的寻找往往结合平面几何的知识，如中位线的性质等；（2）利用面面垂直判定定理证明，即从线面垂直出发给予证明，而线面垂直的证明，往往需要多次利用线面垂直性质定理与判定定理.

试题解析：证明：（1）在直三棱柱中，

在三角形ABC中，因为D，E分别为AB，BC的中点，

所以，于是，

又因为DE平面平面，

所以直线DE//平面.

（2）在直三棱柱中，

因为平面，所以，

又因为，

所以平面.

因为平面，所以.

又因为，

所以.

因为直线，所以

练习册系列答案
相关题目

【题目】对于函数f（x），若f（x0）=x0，则称x0为f（x）的“不动点”，若f[f（x0）]=x0，则称x0为f（x）的“稳定点”，函数f（x）的“不动点”和“稳定点”的集合分别记为A和B，即A={x|f（x）=x}，B={x|f[f（x）]=x}，那么：

（1）函数g（x）=x2-2的“不动点”为______；

（2）集合A与集合B的关系是______．

【题目】已知的三个顶点落在半径为的球的表面上，三角形有一个角为且其对边长为3，球心到所在的平面的距离恰好等于半径的一半，点为球面上任意一点，则三棱锥的体积的最大值为（ ）

A. B. C. D.

【题目】已知函数，．

（1）若函数在区间上存在零点，求实数的取值范围；

（2）当时，若对任意的、，恒成立，求实数的取值范围；

（3）若函数在上的值城为区间，是否存在常数，使得区间的长度为？若存在，求出的值；若不存在，请说明理由．（注：区间的长度为）．

【题目】数列满足，，．

（1）设，证明是等差数列；

（2）求的通项公式．

【题目】等比数列{an}的各项均为正数，且2a1＋3a2＝1， ＝9a2a6.

(1)求数列{an}的通项公式；

(2)设bn＝log3a1＋log3a2＋…＋log3an，求数列的前n项和．

【题目】函数.

（Ⅰ）若曲线在点处的切线与直线垂直，求单调递减区间和极值（其中为自然对数的底数）；

（Ⅱ）若对任意，恒成立.求的取值范围.

【题目】已知函数.

（1）当时，求的单调区间；

（2）若函数在处取得极大值，求实数的取值范围

【题目】2019年4月26日，铁人中学举行了盛大的成人礼.仪式在《相信我们会创造奇迹》的歌声中拉开序幕，庄严而神圣的仪式感动了无数家长，4月27日，铁人中学官方微信发布了整个仪式精彩过程，几十年众志成城，数十载砥砺奋进，铁人中学正在创造着一个又一个奇迹．官方微信发布后，短短几个小时点击量就突破了万人，收到了非常多的精彩留言.学校从众多留言者中抽取了100人参加“学校满意度调查”，其留言者年龄集中在之间，根据统计结果，做出频率分布直方图如下：

（Ⅰ）求这100位留言者年龄的样本平均数和样本方差（同一组数据用该区间的中点值作代表）；

（Ⅱ）由频率分布直方图可以认为，留言者年龄服从正态分布，其中近似为样本均数，近似为样本方差．

(ⅰ)利用该正态分布，求；

（ii）学校从年龄在和的留言者中，按照分层抽样的方法，抽出了7人参加“精彩留言”表彰大会，现要从中选出3人作为代表发言，设这3位发言者的年龄落在区间的人数是，求变量的分布列和数学期望．附：，若，则，.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网