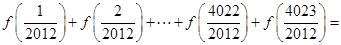题目内容
研究函数的对称中心有如下结论:如果存在实数a, b使![]() 恒成立,则(a, b)为函数
恒成立,则(a, b)为函数![]() 的图像的对称中心.
的图像的对称中心.
(1)求证函数![]() 的图像的对称中心为(0,1),并求函数
的图像的对称中心为(0,1),并求函数![]() 的图象的对称中心;
的图象的对称中心;
(2)试用函数的性质及图象变换解释:“如果存在实数a, b使![]() 恒成立,则(a, b)为函数
恒成立,则(a, b)为函数![]() 的图象的对称中心.”
的图象的对称中心.”
(3)是否存在函数![]() ,使函数
,使函数![]() 的图象有相同的对称中心(c,d)?请对
的图象有相同的对称中心(c,d)?请对![]() 时,说明你的结论与理由.
时,说明你的结论与理由.
解:(1)对于函数![]() 恒成立,
恒成立,
所以![]() 的图象的对称中心为(0,1).
的图象的对称中心为(0,1).
设![]()
![]() 的对称中心为(a,b)
的对称中心为(a,b)
则![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
所以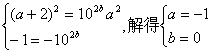
所以![]() 的图象的对称中心为(-1,0)
的图象的对称中心为(-1,0)
(2)由![]()
令![]() 为奇函数,
为奇函数,
其图像关于原点(0,0)对称,
而函数![]() 的图象可由
的图象可由![]() 向右平移a(a>0)或向左平移
向右平移a(a>0)或向左平移![]() 单位或不进行左右平移(a=0),向上平移b(b>0)或向下平移-b(b<0)或不进行上下平移(b=0)单位得到,所以
单位或不进行左右平移(a=0),向上平移b(b>0)或向下平移-b(b<0)或不进行上下平移(b=0)单位得到,所以![]() 的图像的对称中心为(a,b).
的图像的对称中心为(a,b).
说明:(1)中分别说明![]() ,仿(2)也可!
,仿(2)也可!
(3)假设存在函数![]() ,使
,使![]() 有相同的对称中心(c,d)且
有相同的对称中心(c,d)且![]() ,则
,则![]() ,且
,且
![]()
所以![]() 的两个实数,
的两个实数,
而该方程![]() 当
当![]() 时,
时,![]() ,
,
所以假设错误.
所以,不存在函数![]() 有相同的对称中心(c,d),
有相同的对称中心(c,d),
其中![]() .
.

练习册系列答案
相关题目
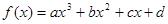
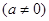 ,给出定义:
,给出定义: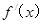 是函数
是函数 的导函数,
的导函数,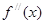 是
是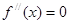 有实数解
有实数解 ,则称点
,则称点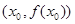 为函数
为函数 的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若
的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数 =________.
=________.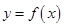 的定义域为
的定义域为 ,若对于任意
,若对于任意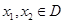 且
且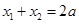 ,恒有
,恒有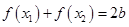 ,则称点
,则称点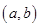 为函数
为函数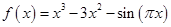 的对称中心,可得
的对称中心,可得