题目内容
(本题12分)在锐角△ABC中,a,b,c分别为角A、B、C所对的边,且![]() a=2csinA,(1)确定角C的大小;(2)若c=
a=2csinA,(1)确定角C的大小;(2)若c=![]() ,且△ABC的面积为
,且△ABC的面积为![]() ,求a+b的值。
,求a+b的值。
(Ⅰ) C=![]() (Ⅱ) 5
(Ⅱ) 5
解析:
(1)由![]() a=2csinA,及正弦定理得,
a=2csinA,及正弦定理得,![]() ,∵sinA≠0,∴sinC=
,∵sinA≠0,∴sinC=![]()
∵△ABC是锐角三角形,∴C=![]()
(2)c= ![]() , C=
, C=![]() ,由面积公式得
,由面积公式得![]() absin
absin![]() =
=![]() ,即ab=6
,即ab=6
由余弦定理得 a2+b2-2abcos![]() =7,即a2+b2-ab=7,则(a+b)2=25,故a+b=5
=7,即a2+b2-ab=7,则(a+b)2=25,故a+b=5

练习册系列答案
相关题目
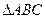 中,已知内角A、B、C所对的边分别为a、b、
中,已知内角A、B、C所对的边分别为a、b、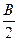 -1)=-
-1)=-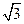 cos2B。
cos2B。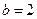 ,求
,求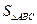 的最大值.
的最大值.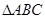 中,
中,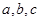 分别为角
分别为角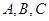 的对边,且
的对边,且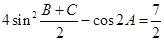 .
.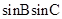 的最大值.
的最大值. 中,已知内角A、B、C所对的边分别为a、b、
中,已知内角A、B、C所对的边分别为a、b、 -1)=-
-1)=- cos2B。
cos2B。 ,求
,求 的最大值.
的最大值.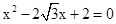 的两根,
的两根, ,求角C的度数,边c的长度及三角形ABO的面积
,求角C的度数,边c的长度及三角形ABO的面积