题目内容
已知二次函数f（x）=x2+bx+c满足：f（x+1）-f（x）=2x，且f（0）=1．
（1）求f（x）的解析式；
（2）求f（x）在区间[0，2]上的最大值与最小值．
解：（1）∵f（0）=1，∴c=1，
∴f（x）=x2+bx+1．
∴f（x+1）-f（x）=（x+1）2+b（x+1）+1-x2-bx-1=2x+b+1=2x
∴b=-1，
∴f（x）=x2-x+1．
（2）
，
∵x∈[0，2]，f（2）=3，
∴f（x）在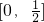
上是减函数，在
上是增函数．
又＞f（0）=1，
∴
．
分析：（1）根据f（0）=1，用待定系数法求得b=-1，即得函数的解析式．
（2）由，可得f（x）在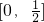上是减函数，在上是增函数，由此求得
函数f（x）在[0，2]上的最值．
点评：本题主要考查求二次函数在闭区间上的最值的方法，用待定系数法求函数的解析式，属于中档题．
∴f（x）=x2+bx+1．
∴f（x+1）-f（x）=（x+1）2+b（x+1）+1-x2-bx-1=2x+b+1=2x
∴b=-1，
∴f（x）=x2-x+1．
（2）
，∵x∈[0，2]，f（2）=3，
∴f（x）在
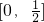上是减函数，在上是增函数．又＞f（0）=1，
∴
． 分析：（1）根据f（0）=1，用待定系数法求得b=-1，即得函数的解析式．
（2）由
，可得f（x）在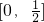上是减函数，在上是增函数，由此求得函数f（x）在[0，2]上的最值．
点评：本题主要考查求二次函数在闭区间上的最值的方法，用待定系数法求函数的解析式，属于中档题．
练习册系列答案
相关题目