题目内容
等腰三角形ABC底边两端点坐标分别为B(4,2)、C(-2,0),则顶点A的轨迹方程是( )
A. | B. |
C. | D. |
C
解析试题分析:设A ,因为|AB|=|AC|,所以
,因为|AB|=|AC|,所以 ,化简得:
,化简得: ,又因为x=1时A、B、C三点共线,所以
,又因为x=1时A、B、C三点共线,所以 ,所以轨迹方程为
,所以轨迹方程为 。
。
考点:求点的轨迹方程。
点评:求曲线的轨迹方程是常见题型,其常采用的方法有直接法、定义法、相关点法、参数法. 我们这里用到的是直接法,即直接列出点A所满足的方程. 不管应用哪种方法求轨迹方程,一定要注意轨迹的纯粹性和完备性.要注意区别“轨迹”与“轨迹方程”是两个不同的概念.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
如果 ,
, ,那么直线
,那么直线 不通过( )
不通过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若直线 经过原点和点A(-2,-2),则它的斜率为
经过原点和点A(-2,-2),则它的斜率为
| A.-1 | B.1 | C.1或-1 | D.0 |
( )过点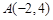 ,且在
,且在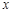 轴上截距是
轴上截距是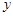 轴上截距的
轴上截距的 倍的直线方程为
倍的直线方程为
A.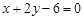 或 或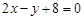 | B.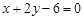 或 或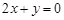 |
C.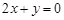 或 或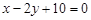 | D.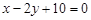 或 或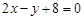 |
已知直线 与曲线
与曲线 在点
在点 处的切线互相垂直,则
处的切线互相垂直,则 的值为( )
的值为( )
A. | B. | C. | D. |
一束光线从点 出发经
出发经 轴反射到圆C:
轴反射到圆C: 上的最短路程是( )
上的最短路程是( )
| A.4 | B.5 | C.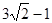 | D. |
直线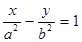 在
在 轴上的截距是( )
轴上的截距是( )
A.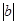 | B.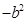 | C.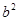 | D.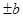 |
已知直线 经过
经过 ,
, 两点,那么直线
两点,那么直线 的倾斜角为( )
的倾斜角为( )
A. | B. | C. | D. |
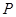 在直线
在直线 上
上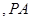 、
、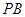 与圆
与圆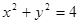 分别相切于
分别相切于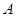 、
、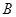 两点
两点 则四边形
则四边形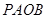 的面积的最小值为( )
的面积的最小值为( )