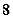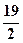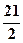题目内容
如图,椭圆中心在坐标原点,F为左焦点,当 时,其离心率为
时,其离心率为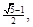 此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( )
此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( ) 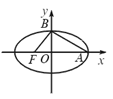
A.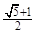 | B. | C.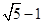 | D.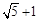 |
A
解析考点:椭圆的简单性质.
分析:类比“黄金椭圆”,在黄金双曲线中,当 时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.
时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.
解:类比“黄金椭圆”,在黄金双曲线中,|OA|=a,|OB|=b,|OF|=c,
当 时,|BF|2+|AB|2=|AF|2,
时,|BF|2+|AB|2=|AF|2,
∴b2+c2+c2=a2+c2+2ac,
∵b2=c2-a2,整理得c2=a2+ac,
∴e2-e-1=0,解得 e=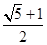 ,或 e=
,或 e=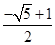 (舍去).
(舍去).
故黄金双曲线的离心率e=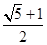 .
.
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知抛物线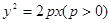 的焦点为
的焦点为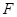 ,
,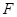 关于原点的对称点为
关于原点的对称点为 过
过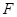 作
作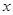 轴的垂线交抛物线于
轴的垂线交抛物线于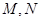 两点.有下列四个命题:①
两点.有下列四个命题:①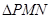 必为直角三角形;②
必为直角三角形;②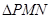 不一定为直角三角形;③直线
不一定为直角三角形;③直线 必与抛物线相切;④直线
必与抛物线相切;④直线 不一定与抛物线相切.其中正确的命题是
不一定与抛物线相切.其中正确的命题是
| A.①③ | B.①④ | C.②③ | D.②④ |
设F1, F2分别为双曲线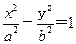 (a>0,b>0)的左、右焦点,P为双曲线右支上任一点。若
(a>0,b>0)的左、右焦点,P为双曲线右支上任一点。若 的最小值
的最小值 为8a,则该双曲线的离心率的取值范围是
为8a,则该双曲线的离心率的取值范围是
A.(1, ] ] | B.(1,3) | C.(1,3] | D.[ ,3) ,3) |
已知点A为双曲线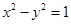 的左顶点,点B和点C在双曲线的右支上,
的左顶点,点B和点C在双曲线的右支上,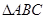 是等边三角形,则
是等边三角形,则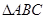 的面积是 ( )
的面积是 ( )
A.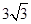 | B.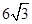 | C.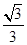 | D. |
已知P是椭圆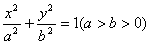 上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
| A.a2 | B.b2 | C.c2 | D.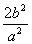 |
若F(c, 0)是椭圆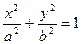 的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于
的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于 的点的坐标是( )
的点的坐标是( )
A.(c, ±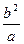 ) ) | B.(-c, ±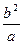 ) ) | C.(0, ±b) | D.不存在 |
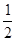 B.x=
B.x=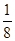 D.y=-
D.y=-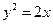 上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( ).
上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( ). 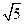
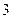
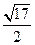
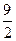
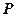 为抛物线
为抛物线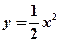 上的动点,点
上的动点,点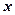 轴上的射影为
轴上的射影为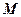 ,点
,点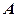 的坐标是
的坐标是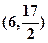 ,则
,则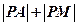 的最小值是 ( )
的最小值是 ( )