题目内容

设[x]表示不超过x的最大整数，如[
5
]=2，[π]=3，[k]=k（k∈N*）．我们发现：
[
1
]+[
2
]+[
3
]=3；
[
4
]+[
5
]+[
6
]+[
7
]+[
8
]=10；
[
9
]+[
10
]+[
11
]+[
12
]+[
13
]+[
14
]+[
15
]=21；
…
通过合情推理，写出一般性的结论：
[
n2
]+[
n2+1
]+[
n2+2
]+…+[
(n+1)2-1
]=n（2n+1）（n∈N*）
[
n2
]+[
n2+1
]+[
n2+2
]+…+[
(n+1)2-1
]=n（2n+1）（n∈N*）
（用含n的式子表示）．
分析：根据条件通过观察，可以得到一个一般性的结论 [
n2
]+[
n2+1
]+[
n2+2
]+…+[
(n+1)2-1
]=n（2n+1）（n∈N*）．
解答：解：根据[
1
]+[
2
]+[
3
]=3；
[
4
]+[
5
]+[
6
]+[
7
]+[
8
]=10；
[
9
]+[
10
]+[
11
]+[
12
]+[
13
]+[
14
]+[
15
]=21；
…
通过观察，发现，等式左边方括号内第一个数是完全平方数，以后依次增加1，最后一个是后一个完全平方数减1，而右边可以写成两个数的积的形式．
我们可以得到一个一般性的结论：[
n2
]+[
n2+1
]+[
n2+2
]+…+[
(n+1)2-1
]=n（2n+1）（n∈N*）．
故答案为：[
n2
]+[
n2+1
]+[
n2+2
]+…+[
(n+1)2-1
]=n（2n+1）（n∈N*）．
点评：本题主要考查的知识点是归纳推理，由特殊的列子得到一般性的结论，属于中档题．
练习册系列答案
相关题目
设[x]表示不超过x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
C
x
n
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，3)时，函数
C
x
8
的值域是（　　）
A、[
16
3
，28]
B、[
16
3
，56)
C、(4，
28
3
)∪[28，56）
D、(4，
16
3
]∪(
28
3
，28]
设[x]表示不超过x的最大整数（如：[1]=1，[
5
2
]=2），则定义在[2，4）的函数f（x）=x[x]-ax（其中a为常数，且a≤4）的值域为（　　）
A、[4-2a，64-4a）
B、[4-2a，9-3a）∪[27-3a，64-4a）
C、[9-3a，64-4a）
D、[4-2a，9-3a]∪（27-3a，64-4a]
（2010•台州二模）设[x]表示不超过x的最大整数（如[2]=2，[1.3]=1），已知函数f(x)=
[x+
1
2
]
[x]+
1
2
（x≥0），当f（x）＜1时，实数x的取值范围是
{x|k≤x＜k+
1
2
，k∈N}
{x|k≤x＜k+
1
2
，k∈N}
．
设[x]表示不超过x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
Cxn
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，3)时，函数C8x的值域是（　　）
A．[
16
3
，28]		B．[
16
3
，56)
C．(4，
28
3
)∪[28，56）		D．(4，
16
3
]∪(
28
3
，28]
设[x]表示不超过x的最大整数，（如[2]=2，=1），对于给定的n∈N+，定义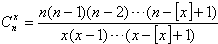，x∈[1，+∞），则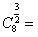（    ），当x∈[2，3）时，函数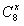的值域是（    ）。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网