题目内容
设f（x）定义在R上的偶函数，且f(x+3)=-| 1 | f(x) |
分析：由f(x+3)=-
可得f（x）是以6为周期的周期函数，则f（2007）=f（6×334+3）=f（3），再由x∈（0，3]时，f（x）=2x求解．
| 1 |
| f(x) |
解答：解：由f(x+3)=-
可得
f(x+6)=-
=f(x)
∴f（x）是以6为周期的周期函数，
又∵又当x∈（0，3]时，f（x）=2x，
∴f（2007）=f（6×334+3）=f（3）=6
故答案为：6
| 1 |
| f(x) |
f(x+6)=-
| 1 |
| f(x+3) |
∴f（x）是以6为周期的周期函数，
又∵又当x∈（0，3]时，f（x）=2x，
∴f（2007）=f（6×334+3）=f（3）=6
故答案为：6
点评：本题主要考查函数的周期性，来转化自变量所在的区间进而来求函数值．
练习册系列答案
相关题目
）=-f（x）；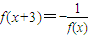
，又当x∈（0，3]时，f（x）=2x，则f（2007）= ．