Question

如图,已知F₁、F₂为双曲线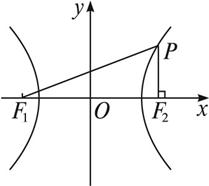(a＞0,b＞0)的焦点,过F₂作垂直于x轴的直线交双曲线于点P,且∠PF₁F₂=30°.求双曲线的渐近线方程.

Answer 1

分析:

由于PF₂⊥x轴,因而可求得P点的纵坐标,即可知|PF₂|的值,结合△PF₁F₂为直角三角形及双曲线的定义,可求得a、b间的关系,就可求得渐近线的斜率.

解法一:

设F₂(c,0)(c＞0),P(c,y₀),

则

∴|PF₂|=.

在Rt△PF₂F₁中,∠PF₁F₂=30°,|F₁F₂|=|PF₂|,即2c=·,将c²=a²+b²代入,

解得b²=2a²,故

∴双曲线的渐近线方程为y=±x.

解法二:设F₂(c,0)(c＞0),P(c,y₀),

则

∴|PF₂|=.

在Rt△PF₂F₁中,∠PF₁F₂=30°,|PF₁|=2|PF₂|,由双曲线的定义可知|PF₁|-|PF₂|=2a,得|PF₂|=2a,

∵|PF₂|=,∴2a=,即b²=2a².

∴

∴双曲线的渐近线方程为y=±2x.

绿色通道：

双曲线上一点P与两焦点F₁、F₂连结形成的△PF₁F₂,是常遇到的一种图形,它往往把三角形的相关知识(如勾股定理、正弦定理、余弦定理、三角形面积公式等)与双曲线的相关知识相结合构造不同的问题,总结对应的解题思路与方法,可从以上的知识入手.