题目内容
设曲线y= 在点(
在点( ,2)处的切线与直线x+ay+1=0垂直,则a=( )
,2)处的切线与直线x+ay+1=0垂直,则a=( )A.2
B.1
C.-1
D.-2
【答案】分析:求出曲线解析式的导函数,把x等于 代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.
代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.
解答:解:y'= ,所以切线斜率k=f′(
,所以切线斜率k=f′( )=1,所以x+ay+1=0的斜率为-1,
)=1,所以x+ay+1=0的斜率为-1,
即- =-1,解得a=1.
=-1,解得a=1.
故选B
点评:此题要求学生会利用导数求曲线上过某点切线方程的斜率,掌握两直线垂直时斜率所满足的关系,是一道综合题.
 代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.
代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.解答:解:y'=
 ,所以切线斜率k=f′(
,所以切线斜率k=f′( )=1,所以x+ay+1=0的斜率为-1,
)=1,所以x+ay+1=0的斜率为-1,即-
 =-1,解得a=1.
=-1,解得a=1.故选B
点评:此题要求学生会利用导数求曲线上过某点切线方程的斜率,掌握两直线垂直时斜率所满足的关系,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
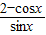 在点(
在点(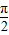 ,2)处的切线与直线x+ay+1=0垂直,则a=( )
,2)处的切线与直线x+ay+1=0垂直,则a=( )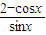 在点(
在点(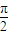 ,2)处的切线与直线x+ay+1=0垂直,则a=( )
,2)处的切线与直线x+ay+1=0垂直,则a=( ) 在点(
在点( ,2)处的切线与直线x+ay+1=0垂直,则a=( )
,2)处的切线与直线x+ay+1=0垂直,则a=( ) 在点(
在点( ,2)处的切线与直线x+ay+1=0垂直,则a=( )
,2)处的切线与直线x+ay+1=0垂直,则a=( )