题目内容
下列命题中:①
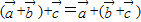
②
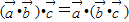 ;
;③函数y=tanx的图象的所有对称中心是(kπ,0),k∈Z;
④函数y=3sin2x的所有对称轴方程为
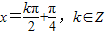 .
.其中正确命题个数是( )
A.0
B.1
C.2
D.3
【答案】分析:根据向量的加法结合律,得①是真命题;根据向量数量积的运算性质,得②是假命题;根据三角函数图象的对称轴和对称中心的公式,建立方程并化简整理,得③为假命题而④是真命题.
解答:解:对于①,根据向量加法的结合律,得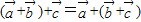 ,故①是真命题;
,故①是真命题;
对于②,因为向量的数量积是一个实数,得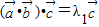 是与
是与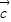 共线的一个向量,
共线的一个向量,
而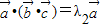 是与
是与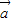 共线的一个向量,所以
共线的一个向量,所以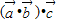 与
与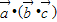 不一定相等,故②是假命题;
不一定相等,故②是假命题;
对于③,满足tan(m+x)=-tan(m-x)的m值的集合为{m|m=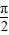 +kπ或m=kπ,k∈Z}
+kπ或m=kπ,k∈Z}
∴函数y=tanx的图象的所有对称中心是( kπ,0),而不是(kπ,0),故③为假命题;
kπ,0),而不是(kπ,0),故③为假命题;
对于④,在函数y=3sin2x中令2x=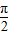 +kπ,k∈Z,得
+kπ,k∈Z,得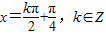 ,
,
故y=3sin2x的所有对称轴方程是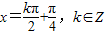 ,得④是真命题.
,得④是真命题.
综上所述,正确命题有①④,共两个
故选:C
点评:本题给出关于向量的运算和三角函数图象对称性的几个命题,判断它们的真假性,着重考查了平面向量的运算性质和三角函数的图象与性质等知识,属于基础题.
解答:解:对于①,根据向量加法的结合律,得
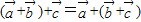 ,故①是真命题;
,故①是真命题;对于②,因为向量的数量积是一个实数,得
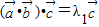 是与
是与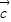 共线的一个向量,
共线的一个向量,而
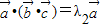 是与
是与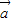 共线的一个向量,所以
共线的一个向量,所以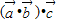 与
与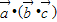 不一定相等,故②是假命题;
不一定相等,故②是假命题;对于③,满足tan(m+x)=-tan(m-x)的m值的集合为{m|m=
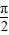 +kπ或m=kπ,k∈Z}
+kπ或m=kπ,k∈Z}∴函数y=tanx的图象的所有对称中心是(
 kπ,0),而不是(kπ,0),故③为假命题;
kπ,0),而不是(kπ,0),故③为假命题;对于④,在函数y=3sin2x中令2x=
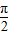 +kπ,k∈Z,得
+kπ,k∈Z,得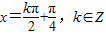 ,
,故y=3sin2x的所有对称轴方程是
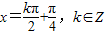 ,得④是真命题.
,得④是真命题.综上所述,正确命题有①④,共两个
故选:C
点评:本题给出关于向量的运算和三角函数图象对称性的几个命题,判断它们的真假性,着重考查了平面向量的运算性质和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
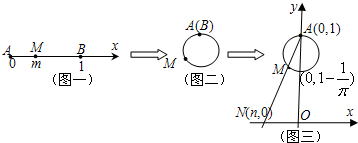 如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )
如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )(1)f(
| 1 |
| 2 |
(2)f(x)是偶函数;
(3)f(x)在其定义域上是增函数;
(4)y=f(x)的图象关于点(
| 1 |
| 2 |
| A、(1)(3)(4) |
| B、(1)(2)(3) |
| C、(1)(2)(4) |
| D、(1)(2)(3)(4) |