题目内容
设![]() 是函数
是函数![]() 的一个极值点。
的一个极值点。
(1)求![]() 与
与![]() 的关系式(用
的关系式(用![]() 表示
表示![]() ),并求
),并求![]() 的单调区间;
的单调区间;
(2)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
解:(1)∵![]()
∴![]()
![]() 2分
2分
由题意得:![]() ,即
,即![]() ,
,![]() 3分
3分
∴![]() 且
且![]()
令![]() 得
得![]() ,
,![]()
∵![]() 是函数
是函数![]() 的一个极值点
的一个极值点
∴![]() ,即
,即![]()
故![]() 与
与![]() 的关系式为
的关系式为![]() 5分
5分
(Ⅰ)当![]() 时,
时,![]() ,由
,由![]() 得单增区间为:
得单增区间为:![]() ;
;
由![]() 得单减区间为:
得单减区间为:![]() 、
、![]() ;
;
(Ⅱ)当![]() 时,
时,![]() ,由
,由![]() 得单增区间为:
得单增区间为:![]() ;
;
由![]() 得单减区间为:
得单减区间为:![]() 、
、![]() ; 8分
; 8分
(2)由(1)知:当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,
,![]()
∴![]() 在
在![]() 上的值域为
上的值域为![]() 10分
10分
易知![]() 在
在![]() 上是增函数
上是增函数
∴![]() 在
在![]() 上的值域为
上的值域为![]() 12分
12分
由于![]() ,
,
又∵要存在![]() ,使得
,使得![]() 成立,
成立,
∴必须且只须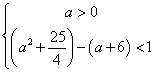 解得:
解得:![]()
所以:![]() 的取值范围为
的取值范围为![]() 14分
14分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 是函数
是函数 的一个极值点.
的一个极值点. 与
与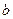 的关系式(用
的关系式(用 的单调区间;
的单调区间;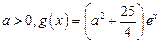 ,若存在
,若存在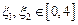 ,使得
,使得 成立,求
成立,求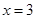 是函数
是函数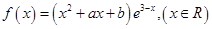 的一个极值点。
的一个极值点。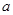 与
与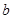 的关系式(用
的关系式(用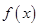 的单调区间;
的单调区间;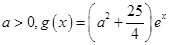 ,若存在
,若存在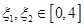 ,使得
,使得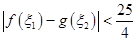 成立,求实数
成立,求实数 是函数
是函数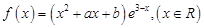 的一个极值点.
的一个极值点. 与
与 的关系式(用
的关系式(用 的单调区间;
的单调区间;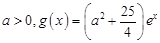 ,若存在
,若存在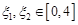 ,使得
,使得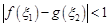 成立,求
成立,求