Question

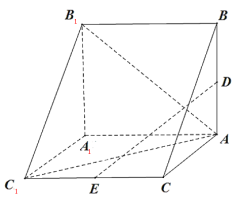
【题目】如图，在棱长为3的正方体ABCDA1B1C1D1中，A1E＝CF＝1.

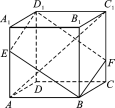
（1）求异面直线AC1与D1E所成角的余弦值；

（2）求直线AC1与平面BED1F所成角的正弦值．

Answer 1

【答案】（1）.（2）

【解析】

（1）先根据题意建立空间直角坐标系，分别求得向量与向量的坐标，再利用线线角的向量方法求解.

（2）先求得平面BED1F的一个法向量，向量的坐标，再利用线面角向量方法求解.

（1） 因为DA，DC，DD1两两垂直，所以分别以DA，DC，DD1所在直线为x轴，y轴，z轴，建立空间直角坐标系，如图所示．

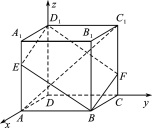
因为棱长为 3， A1E＝CF＝1，

则D(0，0，0)，A(3，0，0)，B(3，3，0)，D1(0，0，3)，C1(0，3，3)，E(3，0，2)，F(0，3，1)．

所以＝(－3，3，3)，＝(3，0，－1)，

所以cos〈〉＝

＝

＝－，

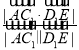
所以异面直线 AC1与 D1E 所成角的余弦值是.

（2）设平面 BED1F的法向量是＝(x,y,z)，

又因为＝(0，－3，2)，＝(－3，0，1)，⊥，⊥，

所以·＝0， ·＝0，

即，令z＝3，

得x＝1，y＝2，所以＝(1，2，3)．

又＝(－3，3，3)，

所以cos〈，〉＝

＝＝，

所以直线 AC1与平面 BED1F 所成角的正弦值为.