题目内容
已知三个函数:①y=2cosx;②y=1-x3;③y=2x+1.其中满足性质:“对于任意x1,x2∈R,若x1<x0<x2, α=| x1+x0 |
| 2 |
| x0+x2 |
| 2 |
分析:根据题意判断出x1<α<β<x2,再根据三个函数的单调性判断出对应函数值的大小,进一步变形判断等式是否成立.
解答:解:∵x1<x0<x2, α=
, β=
,
∴x1<α<β<x2,
∵函数y=1-x3在定义域上是减函数,∴有f(x1)>f(α)>f(β)>f(x2),
∴f(x1)-f(x2)>f(α)-f(β),即|f(α)-f(β)|<|f(x1)-f(x2)|成立;
∵函数y=2x+1在定义域上是增函数,∴f(x1)<f(α)<f(β)<f(x2),
∴f(x2)-f(x1)>f(β)-f(α),即|f(α)-f(β)|<|f(x1)-f(x2)|成立;
由∵函数y=2cosx在定义域上不是单调函数,∴|f(α)-f(β)|<|f(x1)-f(x2)|不成立.
故答案为:②③.
| x1+x0 |
| 2 |
| x0+x2 |
| 2 |
∴x1<α<β<x2,
∵函数y=1-x3在定义域上是减函数,∴有f(x1)>f(α)>f(β)>f(x2),
∴f(x1)-f(x2)>f(α)-f(β),即|f(α)-f(β)|<|f(x1)-f(x2)|成立;
∵函数y=2x+1在定义域上是增函数,∴f(x1)<f(α)<f(β)<f(x2),
∴f(x2)-f(x1)>f(β)-f(α),即|f(α)-f(β)|<|f(x1)-f(x2)|成立;
由∵函数y=2cosx在定义域上不是单调函数,∴|f(α)-f(β)|<|f(x1)-f(x2)|不成立.
故答案为:②③.
点评:本题考查了余弦函数、指数函数和幂函数的单调性的应用,即根据单调性判断对应函数值的大小,这是常用的一种方法.

练习册系列答案
相关题目
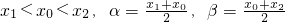 ,则有|f(α)-f(β)|<|f(x1)-f(x2)|成立”的函数是 ________.(写出全部正确结论的序号)
,则有|f(α)-f(β)|<|f(x1)-f(x2)|成立”的函数是 ________.(写出全部正确结论的序号)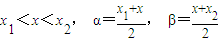 ,则有|f(α)-f(β)|<|f(x1)-f(x2)|成立”的函数是 .(写出全部正确结论的序号)
,则有|f(α)-f(β)|<|f(x1)-f(x2)|成立”的函数是 .(写出全部正确结论的序号)