Question

（本小题满分12分）已知点F是抛物线C：的焦点，S是抛物线C在第一象限内的点，且|SF|=. 

（Ⅰ）求点S的坐标；

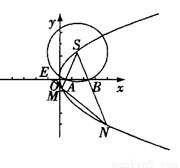
（Ⅱ）以S为圆心的动圆与轴分别交于两点A、B，延长SA、SB分别交抛物线C于M、N两点；

①判断直线MN的斜率是否为定值，并说明理由；

②延长NM交轴于点E，若|EM|=|NE|，求cos∠MSN的值.

 

Answer 1

【答案】

（Ⅰ）(1,1)（Ⅱ）①②

【解析】

试题分析：解：（1）设(＞0)，由已知得F，则|SF|=，

∴=1，∴点S的坐标是(1,1)------------------------2分

（2）①设直线SA的方程为

由得

∴，∴。

由已知SA=SB，∴直线SB的斜率为，∴，

∴--------------7分

②设E(t,0)，∵|EM|=|NE|，∴，

∴ ，则∴--------------------------8分

∴直线SA的方程为，则，同理 

∴---------------------------12分

考点：抛物线的性质；直线的斜率公式；向量的坐标运算；余弦定理。

点评：本题第一小题用了抛物线的性质，这样使问题简化，当然，也可以由两点距离公式来求。第二小题关键要从题意找出直线SA与SB的关系。