题目内容
已知函数f(x)=-x3+x2,g(x)=alnx,a∈R.(1)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求a的取值范围;
(2)设F(x)=
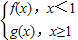 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
【答案】分析:(1)已知对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,可以转化为(x-lnx)a≤x2-2x,再利用系数分离法
(2)假设曲线y=F(x)上存在一点Q(-t,F(-t)),使∠POQ为钝角,则 ,然后对t进行讨论:t<-1,-1<t<1,t>1,三种情况进行讨论,转化为函数的恒成立,利用常数分离法进行求解;
,然后对t进行讨论:t<-1,-1<t<1,t>1,三种情况进行讨论,转化为函数的恒成立,利用常数分离法进行求解;
解答:解:(1)由对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,得(x-lnx)a≤x2-2x,.
由于x∈[1,e],lnx≤1≤x,且等号不能同时取得,所以lnx<x,x-lnx>0.
从而a≤ 恒成立,a≤(
恒成立,a≤( )min. …(4分)
)min. …(4分)
设t(x)= ,x∈[1,e],
,x∈[1,e],
求导,得t′(x)= .…(6分)
.…(6分)
x∈[1,e],x-1≥0,lnx≤1,x+2-lnx>0,
从而t′(x)≥0,t(x)在[1,e]上为增函数.
所以t(x)min=t(1)=-1,所以a≤-1.…(8分)
(2)F(x)= ,
,
设P(t,F(t))为曲线y=F(x)上的任意一点.
假设曲线y=F(x)上存在一点Q(-t,F(-t)),使∠POQ为钝角,
则 ,
,
若t≤-1,P(t,-t3+t2),Q(-t,aln(-t)),
 =-t2+aln(-t)(-t3+t2),
=-t2+aln(-t)(-t3+t2),
由于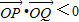 恒成立,a(1-t)ln(-t)<1.
恒成立,a(1-t)ln(-t)<1.
当t=-1时,a(1-t)ln(-t)<1.恒成立.
当t<-1时,a< 恒成立.由于
恒成立.由于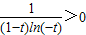 ,所以a≤0.(12分)
,所以a≤0.(12分)
若-1<t<1,t≠0,P(t,-t3+t2),Q(-t,t3+t2),
则 =-t2+(-t3+t2)(t3+t2)<0,
=-t2+(-t3+t2)(t3+t2)<0,
t4-t2+1>0对-1<t<1,t≠0恒成立.…(14分)
③当t≥1时,同①可得a≤0.
综上所述,a的取值范围是(-∞,0]. …(16分)
点评:解决本题的关键在于“转化”,先将转化为恒成立问题,再将将问题转化为二次函数问题,最终得以解决.很多问题在实施“化难为易”、“化生为熟”中得以解决,但是题中所蕴涵的分类讨论思想却是我们常用的方法;
(2)假设曲线y=F(x)上存在一点Q(-t,F(-t)),使∠POQ为钝角,则
 ,然后对t进行讨论:t<-1,-1<t<1,t>1,三种情况进行讨论,转化为函数的恒成立,利用常数分离法进行求解;
,然后对t进行讨论:t<-1,-1<t<1,t>1,三种情况进行讨论,转化为函数的恒成立,利用常数分离法进行求解;解答:解:(1)由对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,得(x-lnx)a≤x2-2x,.
由于x∈[1,e],lnx≤1≤x,且等号不能同时取得,所以lnx<x,x-lnx>0.
从而a≤
 恒成立,a≤(
恒成立,a≤( )min. …(4分)
)min. …(4分)设t(x)=
 ,x∈[1,e],
,x∈[1,e],求导,得t′(x)=
 .…(6分)
.…(6分)x∈[1,e],x-1≥0,lnx≤1,x+2-lnx>0,
从而t′(x)≥0,t(x)在[1,e]上为增函数.
所以t(x)min=t(1)=-1,所以a≤-1.…(8分)
(2)F(x)=
 ,
,设P(t,F(t))为曲线y=F(x)上的任意一点.
假设曲线y=F(x)上存在一点Q(-t,F(-t)),使∠POQ为钝角,
则
 ,
,若t≤-1,P(t,-t3+t2),Q(-t,aln(-t)),
 =-t2+aln(-t)(-t3+t2),
=-t2+aln(-t)(-t3+t2),由于
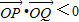 恒成立,a(1-t)ln(-t)<1.
恒成立,a(1-t)ln(-t)<1.当t=-1时,a(1-t)ln(-t)<1.恒成立.
当t<-1时,a<
 恒成立.由于
恒成立.由于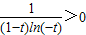 ,所以a≤0.(12分)
,所以a≤0.(12分)若-1<t<1,t≠0,P(t,-t3+t2),Q(-t,t3+t2),
则
 =-t2+(-t3+t2)(t3+t2)<0,
=-t2+(-t3+t2)(t3+t2)<0,t4-t2+1>0对-1<t<1,t≠0恒成立.…(14分)
③当t≥1时,同①可得a≤0.
综上所述,a的取值范围是(-∞,0]. …(16分)
点评:解决本题的关键在于“转化”,先将转化为恒成立问题,再将将问题转化为二次函数问题,最终得以解决.很多问题在实施“化难为易”、“化生为熟”中得以解决,但是题中所蕴涵的分类讨论思想却是我们常用的方法;

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|