题目内容
下列命题中所有正确的序号是 .(1)A=B=N,对应f:x→y=(x+1)2-1是映射;
(2)函数
 和
和 都是既奇又偶函数;
都是既奇又偶函数;(3)已知对任意的非零实数x都有
 ,则f(2)=
,则f(2)= ;
;(4)函数f(x-1)的定义域是(1,3),则函数f(x)的定义域为(0,2);
(5)函数f(x)在(a,b]和(b,c)上都是增函数,则函数f(x)在(a,c)上一定是增函数.
【答案】分析:(1)根据映射的定义进行判断,考虑对应法则;
(2)∵函数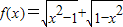 和
和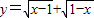 ,根据f(-x)与f(x)的关系进行判断;
,根据f(-x)与f(x)的关系进行判断;
(3)已知对任意的非零实数x都有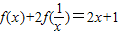 ,令x=
,令x=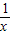 代入,解出f(x),从而求解;
代入,解出f(x),从而求解;
(4)∵函数f(x-1)的定义域是(1,3),即1<x<3,利用整体法进行求解;
(5)根据函数f(x)在(a,b]和(b,c)上都是增函数,因为f(c)点是否连续,不知道,从而不能判断函数f(x)在(a,c)上一定是增函数.
解答:解:(1)A为自然数集,对应法则y=(x+1)2-1,计算结果也是非负整数,对任意x∈N,都有y∈N,故(1)正确;
(2)∵ ,∴f(-x)=f(x)为偶函数,故(2)错误;
,∴f(-x)=f(x)为偶函数,故(2)错误;
(3)∵对任意的非零实数x都有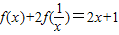 ,
,
∴f(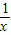 )+2f(x)=
)+2f(x)=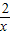 +1,联立方程得:f(x)=-
+1,联立方程得:f(x)=- x+
x+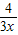 +
+ ,∴f(2)=-
,∴f(2)=- +
+ +
+ =-
=- ;故(3)正确;
;故(3)正确;
(4)∵函数f(x-1)的定义域是(1,3),1<x<3,∴0<x-1<2,∴函数f(x)的定义域为(0,2),故(4)正确;
(5)函数f(x)在(a,b]和(b,c)上都是增函数,若f(x)在c点不连续,就不能说f(x)在(a,c)上一定是增函数,故(5)错误;
点评:此题主要考查映射的定义,奇函数和偶函数的性质,命题(3)是一道好题,注意把x换为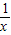 ,使问题迎刃而解,此题综合性比较强.
,使问题迎刃而解,此题综合性比较强.
(2)∵函数
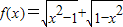 和
和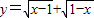 ,根据f(-x)与f(x)的关系进行判断;
,根据f(-x)与f(x)的关系进行判断;(3)已知对任意的非零实数x都有
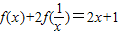 ,令x=
,令x=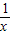 代入,解出f(x),从而求解;
代入,解出f(x),从而求解;(4)∵函数f(x-1)的定义域是(1,3),即1<x<3,利用整体法进行求解;
(5)根据函数f(x)在(a,b]和(b,c)上都是增函数,因为f(c)点是否连续,不知道,从而不能判断函数f(x)在(a,c)上一定是增函数.
解答:解:(1)A为自然数集,对应法则y=(x+1)2-1,计算结果也是非负整数,对任意x∈N,都有y∈N,故(1)正确;
(2)∵
 ,∴f(-x)=f(x)为偶函数,故(2)错误;
,∴f(-x)=f(x)为偶函数,故(2)错误;(3)∵对任意的非零实数x都有
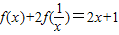 ,
,∴f(
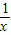 )+2f(x)=
)+2f(x)=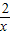 +1,联立方程得:f(x)=-
+1,联立方程得:f(x)=- x+
x+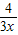 +
+ ,∴f(2)=-
,∴f(2)=- +
+ +
+ =-
=- ;故(3)正确;
;故(3)正确;(4)∵函数f(x-1)的定义域是(1,3),1<x<3,∴0<x-1<2,∴函数f(x)的定义域为(0,2),故(4)正确;
(5)函数f(x)在(a,b]和(b,c)上都是增函数,若f(x)在c点不连续,就不能说f(x)在(a,c)上一定是增函数,故(5)错误;
点评:此题主要考查映射的定义,奇函数和偶函数的性质,命题(3)是一道好题,注意把x换为
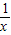 ,使问题迎刃而解,此题综合性比较强.
,使问题迎刃而解,此题综合性比较强. 
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目