题目内容
在△ABC中,角A、B、C所对的边为a、b、c.求证:![]()
证明:由余弦定理a2-b2=c2-2bccosA,
得![]()
又由正弦定理,得
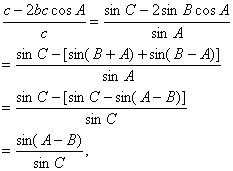
∴![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |
题目内容
在△ABC中,角A、B、C所对的边为a、b、c.求证:![]()
证明:由余弦定理a2-b2=c2-2bccosA,
得![]()
又由正弦定理,得
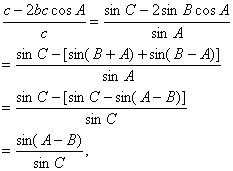
∴![]()

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |