题目内容
(本小题满分12分)
已知函数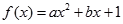 (
(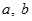 为实数,
为实数,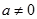 ,
,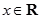 ),若
),若 ,且函数
,且函数 的值域为
的值域为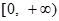 .
.
(1)求 的表达式;
的表达式;
(2)当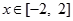 时,
时,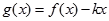 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.
解:
(1)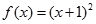 ;(2)
;(2)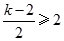 或
或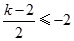 时
时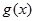 单调。
单调。
解析试题分析:(1)根据题意分析得到函数a,b的关系式, ,所以
,所以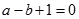 .,同时利用
.,同时利用 的值域为
的值域为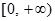 ,说明判别式为零。
,说明判别式为零。
(2)根据对称轴和定义域的关系,来得到参数的范围。
解:
(1)因为 ,所以
,所以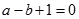 .
.
因为 的值域为
的值域为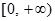 ,所以
,所以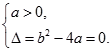 .................3分
.................3分
所以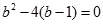 . 解得
. 解得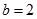 ,
,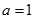 . 所以
. 所以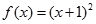 ....................6分
....................6分
(2)因为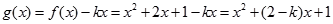
=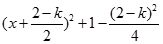 ,..................................8分
,..................................8分
所以当 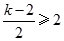 或
或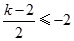 时
时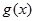 单调.................................12分
单调.................................12分
考点:本试题主要考查了二次函数解析式的求解,以及单调性的运用。
点评:解决该试题的关键是通过函数的值域,得到最小值为0,进而确定出判别式为零。那么再结合对称轴和定义域的关系得到参数的范围。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 (
( 为常数)。
为常数)。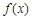 的图象在点(
的图象在点(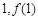 )处的切线与函数
)处的切线与函数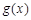 的图象相切,求实数
的图象相切,求实数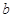 的值;
的值;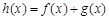 ,若函数
,若函数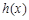 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数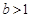 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数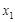 ,
,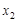 ,都有
,都有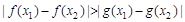 成立,求
成立,求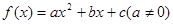 的图象过点
的图象过点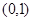 ,且与
,且与 轴有唯一的交点
轴有唯一的交点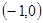 .(1)求
.(1)求 的表达式;
的表达式; 时,求函数
时,求函数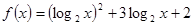 ,
,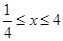 ,
,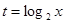 ,求
,求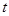 取值范围;
取值范围;  的最值,并给出函数取最值时对应的x的值。
的最值,并给出函数取最值时对应的x的值。 最大值为
最大值为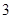 ,且
,且
 的解析式;
的解析式; 上的最值.
上的最值.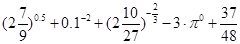
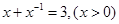 ,求
,求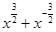 的值.
的值.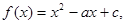 (其中
(其中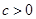 ).
).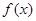 为偶函数,求
为偶函数,求 的值;
的值; ,指出
,指出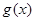 在
在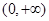 上单调性情况,并证明之.
上单调性情况,并证明之.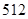 平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,问堆料场的长和宽各为多少时,才能使砌墙所用的材料最省?
平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,问堆料场的长和宽各为多少时,才能使砌墙所用的材料最省?