题目内容
设 是半径为
是半径为 的球面上的四个不同点,且满足
的球面上的四个不同点,且满足 ,
, ,
, ,用
,用 分别表示△
分别表示△ 、△
、△ 、△
、△ 的面积,则
的面积,则 的最大值是( ).
的最大值是( ).
A. | B.2 | C.4 | D.8 |
B
解析试题分析:设 则有
则有 即
即 的最大值为2.
的最大值为2.
考点:基本不等式

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
设 ,且
,且 ,若
,若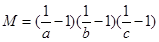 ,则必有
,则必有
A. | B. | C. | D. |
已知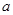 、
、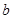 都是正实数,函数
都是正实数,函数 的图象过
的图象过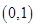 点,则
点,则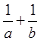 的最小值是( )
的最小值是( )
A.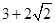 | B.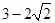 | C.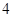 | D. |
设 ,
, ,若
,若 ,则
,则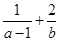 的最小值为( )
的最小值为( )
A.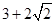 | B.6 | C. | D. |
 、
、 ,“
,“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
已知不等式 的解集为
的解集为 ,点
,点 在直线
在直线 上,其中
上,其中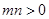 ,则
,则 的最小值为( )
的最小值为( )
A. | B.8 | C.9 | D.12 |
已知 ,则
,则 的最小值是( )
的最小值是( )
| A.4 |
| B.3 |
| C.2 |
| D.1 |
某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则x=( )
| A.20 | B.10 | C.16 | D.8 |
 取得最小值时,x+2y﹣z的最大值为( )
取得最小值时,x+2y﹣z的最大值为( )
