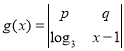题目内容

【题目】已知函数，且在处的切线方程为.

（1）求的解析式，并讨论其单调性.

（2）若函数，证明：.

【答案】（1）见解析（2）见解析

【解析】

（1）先求出切点的坐标，通过切线方程可以求出切线的斜率，对函数进行求导，

求出切线方程的斜率，这样得到一个等式，最后求出的值，这样就求出的解析式。求出定义域，讨论导函数的正负性，判断其单调性。

（2）研究的单调性，就要对进行求导，研究导函数的正负性，就要对进行求导，得到，研究的正负性，从而判断出的单调性，进而判断出的正负性，最后判断出的单调性，利用单调性就可以证明结论。

（1）由题切点为代入得：①

即②

解得，

∴，，

∴，即为上的增函数.

（2）由题，即证，

.

构造函数，，

，即为上的增函数，

又，即

时，即在上单调递减，

时，，即在上单调递增，

∴得证.

练习册系列答案
相关题目

【题目】已知函数f(x)＝|2x－a|＋|2x－1|(a∈R).

(1)当a＝－1时，求f(x)≤2的解集；

(2)若f(x)≤|2x＋1|的解集包含集合，求实数a的取值范围.

【题目】已知椭圆的离心率为，焦距为.斜率为k的直线l与椭圆M有两个不同的交点A，B.

（Ⅰ）求椭圆M的方程；

（Ⅱ）若，求 的最大值；

（Ⅲ）设，直线PA与椭圆M的另一个交点为C，直线PB与椭圆M的另一个交点为D.若C,D和点 共线，求k.

【题目】已知矩形，，，将沿矩形的对角线所在的直线进行翻折，在翻折过程中，则（ ）．

A. 当时，存在某个位置，使得

B. 当时，存在某个位置，使得

C. 当时，存在某个位置，使得

D. 时，都不存在某个位置，使得

【题目】已知，函数且.

（1）求p,q的值以及函数的表达式，并写出的定义域D；

（2）设函数，A=，集合，当时，求实数k的取值范围；

（3）当时，设，数列的前n项和为，直线的斜率为，是否存在实数，使对一切恒成立，若存在，分别求出实数的取值范围，若不存在，说明理由.

【题目】已知椭圆：的右焦点为，离心率为，是椭圆上位于第一象限内的任意一点，为坐标原点，关于的对称点为，，圆：.

（1）求椭圆和圆的标准方程；

（2）过点作与圆相切于点，使得点，点在的两侧.求四边形面积的最大值.

【题目】如图，P是圆x2+y2＝4上的动点，P点在x轴上的射影是D，点M满足．

（Ⅰ）求动点M的轨迹C的方程

（Ⅱ）设A、B是轨迹C上的不同两点，点E（﹣4，0），且满足，若λ∈[，1），求直线AB的斜率k的取值范围．

【题目】在直角坐标系中，曲线（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为 曲线的极坐标方程为，与交于点.

（1）写出曲线的普通方程及直线的直角坐标方程，并求；

（2）设为曲线上的动点，求面积的最大值.

【题目】在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为 ，过点的直线的参数方程为（为参数），与交于两点

(1) 求的直角坐标方程和的普通方程；

(2) 若,,成等比数列，求的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网