题目内容
已知函数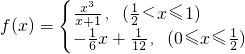 和函数
和函数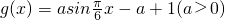 ,若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是
,若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是
- A.
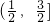
- B.[1,2)
- C.

- D.
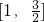
C
分析:根据已知函数f(x)的定义域,求出其值域,对于g(x)利用导数求出其值域,已知存在x1,x2∈[0,1],使得f(x1)=g(x2),可知g(x)的最大值大于等于f(x)的最小值,g(x)的最小值小于等于f(x)的最大值;
解答:函数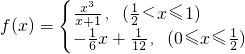 ,
,
当 <x≤1时,f(x)=
<x≤1时,f(x)= ,f′(x)=
,f′(x)=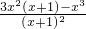 =
=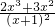 >0,
>0,
f(x)为增函数,∴f( )<f(x)≤f(1),
)<f(x)≤f(1),
∴f(x)∈( ,
, ];
];
当0≤x≤ 时,f(x)=-
时,f(x)=- x+
x+ ,为减函数,
,为减函数,
∴f( )≤f(x)≤f(0),
)≤f(x)≤f(0),
∴f(x)∈[0, ],
],
综上:f(x)∈[0, ];
];
函数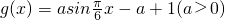 ,g′(x)=
,g′(x)=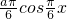 ,0≤
,0≤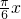 ≤
≤ ,
,
∴g′(x)>0;
g(x)为增函数,g(0)≤g(x)≤g(1),
∴g(x)=[1-a,1- ],
],
∵存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,
∴g(x)的最大值大于等于f(x)的最小值,g(x)的最小值小于等于f(x)的最大值,
∴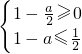 解得
解得 ≤a≤2,
≤a≤2,
故选C;
点评:此题主要考查函数的存在性问题,一般与恒成立问题一个类型,知识点比较全面,是一道中档题,也是一道好题;
分析:根据已知函数f(x)的定义域,求出其值域,对于g(x)利用导数求出其值域,已知存在x1,x2∈[0,1],使得f(x1)=g(x2),可知g(x)的最大值大于等于f(x)的最小值,g(x)的最小值小于等于f(x)的最大值;
解答:函数
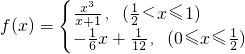 ,
,当
 <x≤1时,f(x)=
<x≤1时,f(x)= ,f′(x)=
,f′(x)=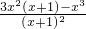 =
=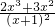 >0,
>0,f(x)为增函数,∴f(
 )<f(x)≤f(1),
)<f(x)≤f(1),∴f(x)∈(
 ,
, ];
];当0≤x≤
 时,f(x)=-
时,f(x)=- x+
x+ ,为减函数,
,为减函数,∴f(
 )≤f(x)≤f(0),
)≤f(x)≤f(0),∴f(x)∈[0,
 ],
],综上:f(x)∈[0,
 ];
];函数
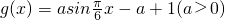 ,g′(x)=
,g′(x)=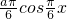 ,0≤
,0≤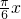 ≤
≤ ,
,∴g′(x)>0;
g(x)为增函数,g(0)≤g(x)≤g(1),
∴g(x)=[1-a,1-
 ],
],∵存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,
∴g(x)的最大值大于等于f(x)的最小值,g(x)的最小值小于等于f(x)的最大值,
∴
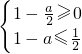 解得
解得 ≤a≤2,
≤a≤2,故选C;
点评:此题主要考查函数的存在性问题,一般与恒成立问题一个类型,知识点比较全面,是一道中档题,也是一道好题;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目