Question

求圆心在直线x+y=0上,且过两圆x²+y²-2x+10y-24=0与x²+y²+2x+2y-8=0交点的圆的方程.

Answer 1

思路点拨：对于这种类型的题目一般有两种处理方法:一是求出交点坐标;二是回避求交点坐标,利用圆系方程的特点来求.

解法一：解方程组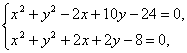

得交点分别为(0,2)、(-4,0).

设所求圆心坐标为(a,-a),则根据圆的性质有==r(圆的半径).解得a=-3,r=.

因此所求圆的方程为(x+3)²+(y-3)²=.

解法二：设所求圆的方程为

x²+y²-2x+10y-24+λ(x²+y²+2x+2y-8)=0(λ≠-1).

整理得(1+λ)x²+(1+λ)y²+2(λ-1)x+2(λ+5)-8λ-24=0.

因为这个圆的圆心在直线x+y=0上,所以=0.

解得λ=-2.

代入即可得所求圆的方程为

x²+y²+6x-6y+8=0.

［一通百通］ 求过两圆交点的圆的方程通常有两种思路:求交点法、利用圆系方程法.前者需要解一个二元二次方程组,需要注意准确性;后者只需解一个方程,但是要注意化简方程时的准确性.相比之下,第二种方法更好些.